Probability Theory & Trading

What Is Probability Theory and Why Is It Important?

Probability theory is essential in trading and investing because it allows market participants to understand and quantify the uncertainty and risk associated with financial decisions.

Like life itself, trading is about probabilities. There are rarely black-and-white obvious outcomes that are easy to capitalize on.

By using probability theory, traders/investors can make more informed decisions based on the likelihood of various outcomes.

Here are a few reasons why probability theory is so important in trading/investing:

Quantifying Risk

Probability theory allows investors to calculate the probability of various things happening, including both positive and negative scenarios.

This enables traders to better understand the potential risks associated with different trades/investments.

Decision Making

Probability theory allows traders to make better decisions based on the probability of different outcomes and assessing the probabilities themselves (what you might call “probabilities of probabilities” as the odds of various things happening aren’t known themselves).

For example, if an investment/trade has a 70% probability of producing a positive return over one year’s time, how do you know that?

Probability theory covers things like variance and how to better handle what you don’t know and can’t know.

Portfolio Management

Probability theory helps traders/investors to manage their portfolios by providing a way to evaluate the risk associated with different asset classes.

By analyzing the probability of different outcomes, traders/investors can create a diversified portfolio that balances risk and return.

Risk Management

Probability theory is also important in risk management, helping investors to determine the likelihood of events that could negatively impact their investments/trades and take steps to mitigate them.

Overall, probability theory is an important tool for investors/traders to understand the risks and potential rewards of different investment opportunities, make more informed choices, and achieve better outcomes over the long term.

In this article, we’ll look at the various branches of probability theory and its applications in trading.

Randomness

In probability theory, randomness refers to the fact that the outcome of an event is unpredictable and can vary from one trial to the next.

This is often modeled using probability distributions, which describe the likelihood of each possible outcome.

Randomness is a fundamental concept in probability theory because it allows us to quantify what’s unknown and make predictions about the future based on incomplete information.

In many real-world situations, the outcomes of events are affected by a large number of variables that are difficult or impossible to predict with certainty/precision.

Randomness provides a way to account for this and to estimate the probability of various outcomes based on historical data, economic cause-effect linkages, or other information.

In trading/investing, randomness is always there because financial markets are subject to a wide range of influences.

You have many different types of people in markets, with different sizes, and with different motivations for why they’re transacting.

Randomness can manifest in the form of market volatility, unexpected news events, or other factors that can cause prices to fluctuate rapidly and unpredictably.

Understanding and accounting for this randomness is critical to developing successful trading strategies and managing risk.

The more experience people get in markets, the more they realize that whatever it is that they know is low in relation to the things that you need to know in relation to what’s discounted into markets.

One way that traders and investors can deal with randomness is by using probability-based models to make decisions.

For example, a trader might use a statistical model to estimate the probability of a particular asset increasing or decreasing in price over a given time period. This information can then be used to make a well-rounded portfolio and manage risk.

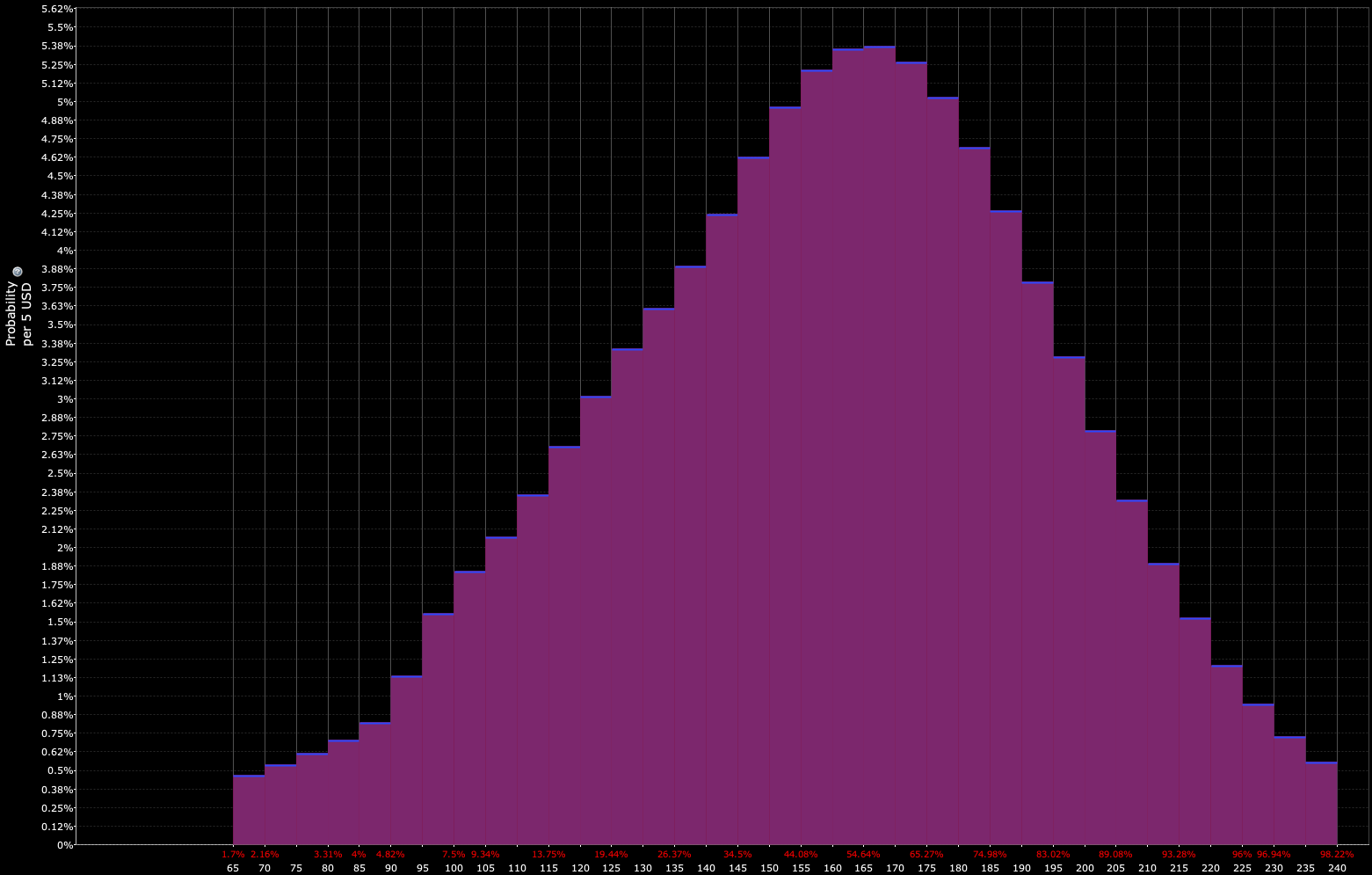
For instance, if the discounted price distribution of a particular asset looks like this:

And the trader’s interpretation is closer to the combination of the red and purple distribution (i.e., a bearish slant):

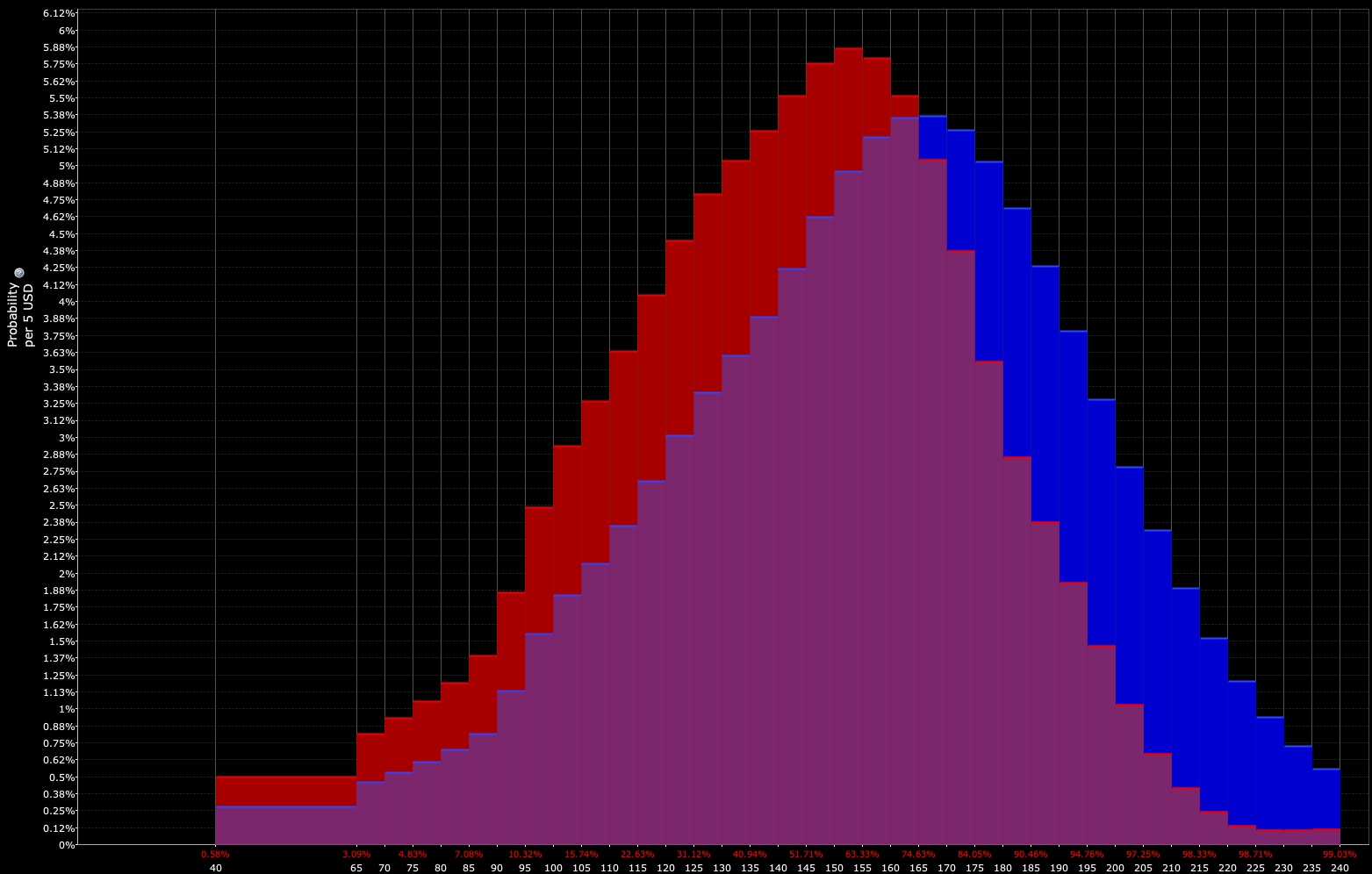
Then they might expect to take some type of bearish position on the asset. Then, of course, there’s the matter of how to put it on and the sizing.

Mutual Exclusivity

In probability theory, the concept of mutual exclusivity refers to the property of two events that are different from each other.

Mathematically, two events A and B are said to be mutually exclusive if their intersection (i.e., the event where both A and B occur) is empty, i.e., P(A ∩ B) = 0.

Mutual exclusivity is important in trading/investing because it helps investors better understand how to manage their risks.

When investors hold a portfolio of assets, they need to consider the correlations between/among their assets.

For example, let’s say a trader/investor has a portfolio of stocks that includes both technology companies and oil companies. If the price of oil goes up, this may help the oil companies but the technology stocks may suffer (i.e., due to the adverse effect of higher oil prices causing a rise in interest rates), and vice versa.

However, if certain developments in each industry occur, they may not have an influence on the prices of the securities from the other industry.

So even though the securities are connected to each other in some ways – such as changes in discounted growth and inflation – in other ways they are mutually exclusive.

How are these mutually exclusive factors separated out?

Sometimes it is simply the nature of the cash flow – e.g., oil vs. tech products/services.

Sometimes they’re known as factors – e.g., momentum, size, quality, value, etc.

Furthermore, mutual exclusivity is important in options trading, where the payoff of one option can often be based on the non-occurrence of another event. In this context, mutual exclusivity helps traders to hedge their risks and manage their exposures.

Probability in Finance – Statistics For The Trading Floor – Quantitative Methods

Experiment (Bernoulli Trial)

An experiment or Bernoulli trial is a fundamental concept in probability theory that refers to a random event with only two possible outcomes.

For example, the toss of a coin is a Bernoulli trial, where the possible outcomes are heads or tails.

Another example is whether a particular option trade will payoff (land in-the-money) or not (land out-of-the-money) by expiration.

In probability theory, the probability of success (i.e., the outcome we’re interested in) is defined as p, and the probability of failure (i.e., the other outcome) as q = 1 – p.

The outcomes of a Bernoulli trial are often denoted by 1 for success and 0 for failure.

The importance of Bernoulli trials in trading and investing lies in the fact that some financial decisions involve binary outcomes.

For example, you might decide to buy a stock option with the hope that it will land ITM, or you might choose to sell it with the expectation that its price will land OTM and you collect the full premium.

In both cases, the outcome is binary in terms of the moneyness. Pure binary bets come in the form of binary options.

By applying the principles of probability theory to trading and investing, you can make more informed decisions about when to buy or sell.

There are also concepts like expected value that teach you not to always bet on the outcome that’s the most probable.

Probability Distribution

In probability theory, a probability distribution is a function that describes the likelihood of different outcomes in a random experiment or process.

It specifies the probabilities of all possible outcomes of an event, and the sum of probabilities of all the outcomes is equal to one.

There are many types of probability distributions, but some of the most common ones include the normal distribution, the binomial distribution, and the Poisson distribution.

Each distribution has its own set of parameters that determine its shape, and these parameters are often used to make predictions and make decisions.

Of course, in financial markets, returns tend to have fatter tails and not cleanly fit any prepackaged distribution, so they tend to be customized.

Overall, probability distributions are important because they provide a framework for understanding the risk and uncertainty associated with financial investments.

One of the most important concepts in trading/investing is that everything is a probability (i.e., a distribution of potential outcomes). There is no one single outcome that’s particularly likely.

By using probability distributions, traders and investors can estimate the likelihood of different outcomes and make more informed decisions about how to allocate their resources.

For example, a trader might use the normal distribution or a more fat-tailed distribution to model the daily returns of a particular stock.

They could then use this distribution to estimate the probability of the stock’s return exceeding a certain threshold, such as a +/-5% return in a day.

By using probability distributions in this way, traders can better manage their risk and optimize their returns.

In addition to estimating probabilities, probability distributions are also used to create financial instruments such as options and futures contracts.

These instruments are priced based on the underlying distribution of the asset they are linked to, and traders can use them to hedge their risk or make bets on the future price movements of the asset.

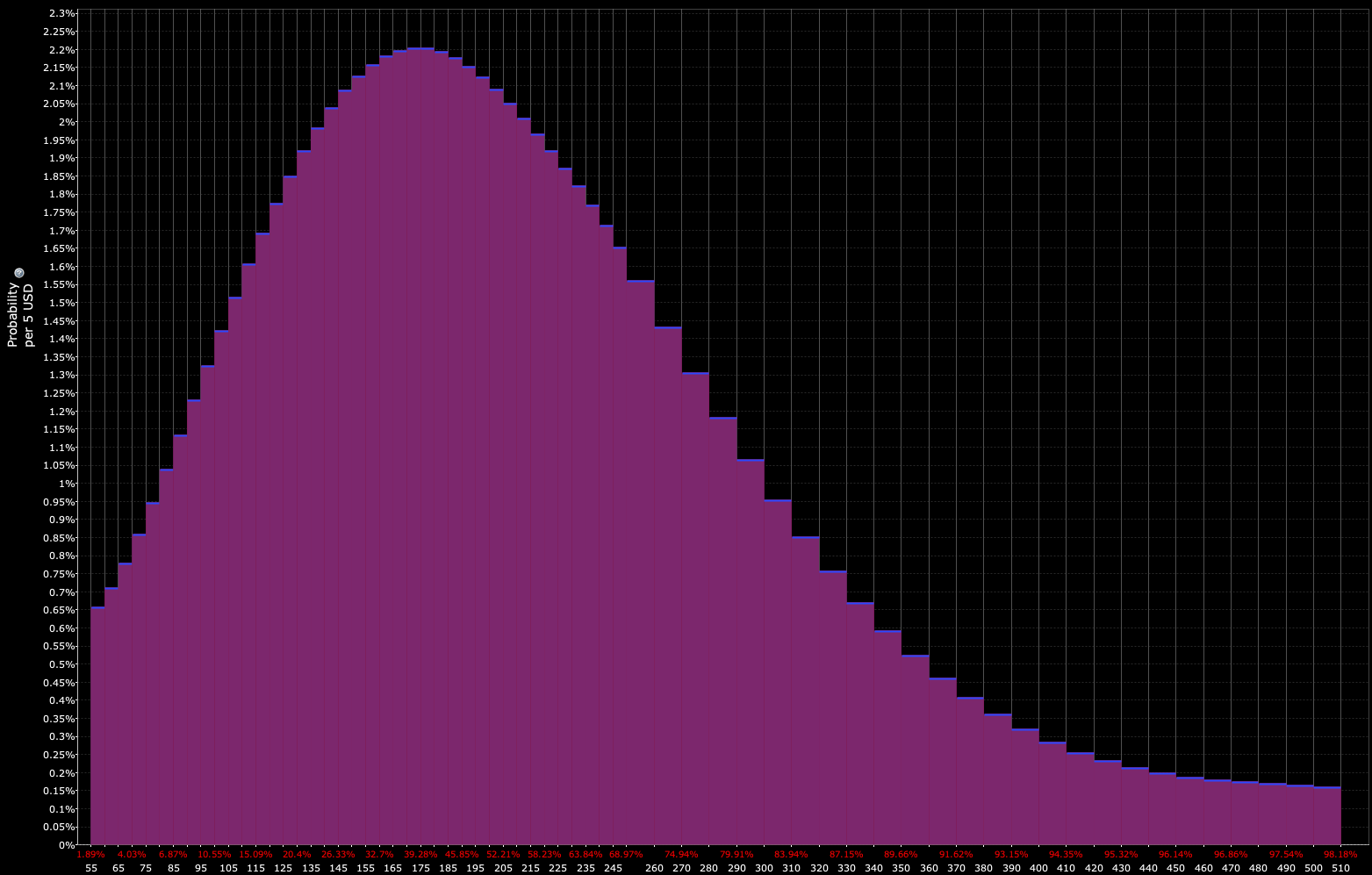
Moreover, distributions can be built out based on the underlying options pricing, such as what’s seen below.

Distribution as discounted by markets:

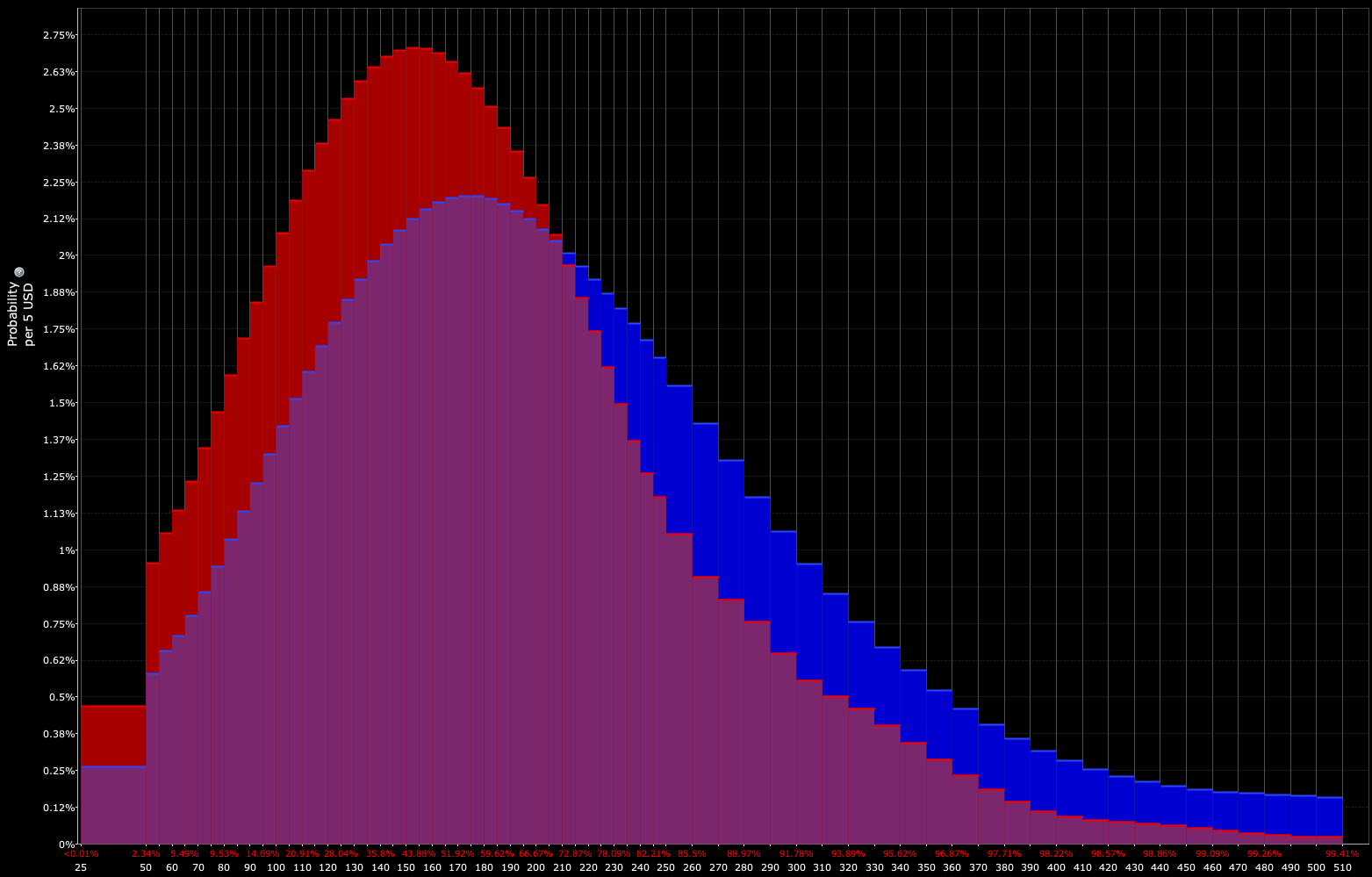
Distribution as determined by trader (which opens the door for tactical opportunities):

Binomial Distribution

The binomial distribution is a probability distribution that models the number of successful outcomes in a series of independent, identical trials, where each trial has only two possible outcomes (e.g., heads or tails, win or lose, up or down).

The key parameters of the binomial distribution are the probability of success in a single trial (denoted by p) and the number of trials (denoted by n).

The binomial distribution is important in trading and investing because it can be used to model the distribution of returns for a binary trading strategy (e.g., a strategy that involves buying or selling an asset based on whether a certain event occurs or not).

In particular, the expected value of a binary trading strategy can be calculated using the binomial distribution.

The expected value of a binary trading strategy is the sum of the products of the probability of each possible outcome and the corresponding return for that outcome.

For example, if a binary trading strategy has a 60% probability of making a 10% return and a 40% probability of making a -5% return, then the expected value of the strategy is:

(0.6 * 0.1) + (0.4 * (-0.05)) = +0.04

The binomial distribution can be used to calculate the probabilities of each possible outcome in a series of binary trades.

For example, if a trader makes 10 binary trades with a 60% probability of success and a 40% probability of failure, the probability of making a certain number of successful trades (i.e., a certain success rate) can be calculated using the binomial distribution.

This can help the trader assess the risk and potential return of their trading strategy.

How Understanding Probability Is IMPORTANT For Trading! (With Examples)

Expected Value

We’ve discussed expected value (EV) in other articles, as it’s a fundamental concept in probability theory that describes the average outcome of a random variable.

In trading and investing, expected value is used to calculate the potential return and risk of an investment or trading strategy.

Mathematically, the expected value of a random variable is the sum of the products of each possible outcome and its probability.

For example, consider a coin flip that pays $1 for heads and $0 for tails.

The expected value of this coin flip is:

EV = (0.5 * $1) + (0.5 * $0) = $0.50

This means that the average payout for this coin flip is $0.50. This will result in breakeven results over time because your odds match the actual probability.

In trading and investing, expected value is used to estimate the potential returns of a trading strategy or investment.

For example, if a stock has a 60% chance of increasing in value by 10% and a 40% chance of decreasing in value by 5%, the expected return of the investment can be calculated as:

EV = (0.6 * 10%) + (0.4 * -5%) = 6% – 2% = 4%

This means that the expected return of the investment is 4%.

This information can help investors and traders decide whether to invest in the stock, and to assess the risk and potential return of their investment.

Expected value is also important in risk management.

By calculating the expected value of a trading strategy or investment, traders and investors can assess the potential risk of the investment.

For example, if the expected value of an investment is negative, this means that the investment is likely to lose money on average over the long run.

Traders/investors can use this information to manage their risk by diversifying their investments or by limiting their exposure to the investment or trade.

Moreover, as we’ve also discussed in other articles, betting on the highest expected value outcome is not always the best decision.

Sometimes having lower EV is better if it gives you lower variance (lower risk of loss or failure). Moreover, you always want to make sure you can cover the loss.

For example, if you have $1,000 and a 90% chance of doubling your money to $2,000 and a 10% chance of losing the entire $1,000, your EV is very high ($1,800 – $1,000 = +$800).

But if you can’t afford to lose the $1,000 in the event you are wrong, then are best to not go through with the decision.

Markov Chain

Markov Chain is a mathematical concept in probability theory that describes a process where the next step or state depends only on the current state and not on any previous states.

In other words, it’s a memoryless process that only relies on its current state to determine its future state.

A Markov Chain is defined by a set of states, and the probabilities of moving from one state to another.

These probabilities are often represented in a transition matrix, where each element in the matrix represents the probability of moving from one state to another.

Markov Chain is important in trading/investing because it can be used to model the behavior of financial markets.

The stock market, for example, is a complex system with a large number of variables affecting the price of securities within it.

Markov Chain provides a way to simplify the system by focusing only on the current state of the market and the probabilities of moving to other states.

By modeling the stock market as a Markov Chain, traders and investors can potentially gain an additional perspective by predicting future market movements based on the current state of the market.

Markov Chain can also be used to help calculate various metrics such as expected returns, volatility, and risk.

Furthermore, Markov Chain is used in various financial modeling techniques such as option pricing, portfolio optimization, and risk management.

It allows traders/investors to create and test different investment strategies, and to measure the effectiveness of these strategies under different market conditions.

Random Walk

Random walk is a mathematical concept in probability theory that describes the movement of an object in a random and unpredictable way.

In a random walk, the next position of the object is determined by a random process, such as a coin toss or a roll of a die.

In finance, a random walk model is often used to describe the movement of stock prices over time.

The theory behind this model is that the movement of stock prices is unpredictable and follows a random pattern.

This means that the price of a stock at any given time is equally likely to go up or down, and the movement of the stock price over time is not influenced by past prices or other external factors. (Of course, there are various ideas and theories about trends, momentum, etc.)

The concept of random walk is useful to know in trading and investing because it suggests that it is very difficult to predict the movement of stock prices.

This means that it is challenging to consistently beat the market by buying and selling stocks based on past price movements or other information.

Investors and traders can use the concept of random walk to inform their investment strategy and make more informed decisions.

For example, they may choose to invest in a diversified portfolio of stocks to reduce their exposure to individual stock price movements and diversifying by assets, asset classes, countries, and currencies, and consider the use of a buy-and-hold strategy to avoid the costs and risks of frequent trading.

Trading: A Game of Probability

Stochastic Process

Stochastic process is a mathematical framework used to model the behavior of a system that evolves randomly over time.

It is a collection of random variables indexed by time, which means that the value of the process at any given time is random.

Stochastic processes are useful in probability theory because they can help us analyze the behavior of random phenomena that change over time.

They provide a way to model and understand the randomness of these phenomena, which can be used to make predictions and make decisions based on the expected outcomes.

In trading and investing, stochastic processes are used to model some of the behavior of financial markets and asset prices.

They provide a way to analyze the randomness and volatility of financial data, which can be used to make decisions about when to buy or sell assets.

For example, stochastic processes can be used to model the movement of stock prices or currency exchange rates, which can help traders and investors make predictions about future movements in these markets.

Stochastic processes are also used to develop and test trading strategies. By simulating the behavior of financial markets using stochastic processes, traders and investors can test their trading strategies and evaluate their performance under different market conditions.

Conditional Probability

Conditional probability is a fundamental concept in probability theory that refers to the likelihood of an event occurring given that another event has already occurred. It is a way of updating our probability estimates based on new information.

More formally, the conditional probability of an event A given that event B has occurred is defined as:

P(A | B) = P(A and B) / P(B)

Where:

• P(A and B) is the probability that both events A and B occur, and
• P(B) is the probability of event B occurring

Conditional probability is important in trading and investing because it allows us to update our probability estimates as new information becomes available.

For example, if we know that a company has just announced a positive earnings report, the conditional probability of the stock price increasing given this information is higher than it was before the announcement.

Investors and traders use conditional probability to make better-informed decisions based on new information.

By updating their probability estimates, they can better assess the risks and potential rewards of a given investment.

This can help them make more profitable trades and manage their risk more effectively.

For example, suppose an investor is considering buying a stock that has historically been volatile.

By using conditional probability, the investor can assess the likelihood of the stock price increasing or decreasing given various market conditions, such as changes in interest rates, growth, inflation, policy, or geopolitical events.

This information can help the investor make a more informed decision about whether to buy, hold, or sell the stock.

Law of Large Numbers

The Law of Large Numbers is a fundamental concept in probability theory that describes the behavior of the average of a large number of independent random variables.

The law states that as the number of independent trials increases, the average of those trials will converge to the expected value of the underlying probability distribution.

In simpler terms, the Law of Large Numbers states that the more times an experiment is repeated, the closer the observed results will be to the expected outcome.

Coin Flip Example

For example, if a coin is flipped repeatedly, the Law of Large Numbers predicts that the frequency of heads will approach 50% as the number of coin flips increases.

Over 1,000 trials it’s extremely improbable for a fair coin to go 55/45 one way or another (0.17%), though it’s definitely possible over 100 flips (36.8%).

Why It’s Useful

The Law of Large Numbers is useful in trading and investing because it helps to mitigate the risk of unpredictable market fluctuations.

By investing in a diversified portfolio, an investor can spread their risk across a large number of assets, which can help to reduce the impact of individual asset price movements.

Additionally, the Law of Large Numbers is useful in analyzing historical market data to make informed investment decisions.

By examining a large number of historical market trends, investors can help identify patterns and trends that can help them to make more informed investment decisions.

For instance, if a trader wanted to know if the Federal Reserve has ever cut interest rates despite inflation being above their target, they could look toward history to see if there are any precedents and the effect it had on various asset markets.

If there is a sample, how big is it to get enough useful data to determine useful conclusions?

How is the Law of Large Numbers related to statistical significance?

The Law of Large Numbers and statistical significance are related concepts in statistics, but they are not the same thing.

The Law of Large Numbers refers to the fact that the sample mean of a large number of independent observations will converge to the expected value of the underlying probability distribution, as the number of observations approaches infinity.

Statistical significance, on the other hand, is a measure of the likelihood that the observed results of a study are not due to chance.

In statistical hypothesis testing, a result is considered statistically significant if the probability of obtaining the observed result by chance is lower than a pre-specified threshold, typically 5% or less.

In practice, the Law of Large Numbers can be used to support statistical significance.

When a large sample is collected and the sample mean is close to the expected value of the underlying distribution, this suggests that the observed results are less likely to be due to chance and more likely to be statistically significant.

However, it’s important to note that statistical significance does not necessarily imply practical significance or economic relevance, and that statistical significance alone should not be used to make important decisions.

A thorough understanding of the underlying data, statistical methods, and the context of the problem being studied is crucial for making well-informed decisions.

Bayes Theorem

Bayes Theorem is a fundamental concept in probability theory that describes how to update probabilities based on new evidence or information.

It is named after the Reverend Thomas Bayes, an 18th-century British statistician and theologian.

The theorem provides a way to calculate the probability of a hypothesis or event based on prior knowledge or beliefs (called the prior probability) and new evidence (called the likelihood).

The updated probability is called the posterior probability, and it represents the probability of the hypothesis or event after taking into account the new evidence.

The formula for Bayes Theorem is:

P(A|B) = P(B|A) * P(A) / P(B)

Where:

• P(A|B) is the posterior probability of event A given evidence B
• P(B|A) is the likelihood of evidence B given event A
• P(A) is the prior probability of event A, and
• P(B) is the probability of evidence B

Bayes Theorem is useful in trading and investing because it can help investors update their beliefs about the likelihood of different events based on new information, such as news about a company’s earnings or economic indicators.

And that’s a key aspect of Bayesian probability – it updates your prior beliefs, it does not necessarily determine or recalculate them from scratch.

By using Bayes Theorem, investors can update their probabilities and make more informed investment decisions.

Examples of the Importance of Stress-Testing Our Assumptions

Bank teller

One famous example of Bayes Theorem in action comes from the Kahneman and Tversky study.

In the study, participants were given the following information:

Linda is 31 years old, single, outspoken, and very bright. She majored in philosophy. As a student, she was deeply concerned with issues of discrimination and social justice, and also participated in anti-nuclear demonstrations.

Participants were then asked to rank the likelihood of two possible scenarios:

• Linda is a bank teller.
• Linda is a bank teller and is active in the feminist movement.

Despite the fact that the first scenario includes more people (all bank tellers) than the second scenario (bank teller and feminist), many participants ranked the second scenario as more likely.

This is because the description of Linda fits with their stereotype of a feminist, even though the likelihood of both events happening is lower than just the likelihood of the first event.

This example demonstrates the importance of stress-testing our assumptions and considering all available information before making decisions.

Bayes Theorem can help investors update their probabilities and avoid biases that may lead to incorrect decisions.

Is Steve a farmer or librarian?

The famous study conducted by Kahneman and Tversky involved another scenario where participants were asked to determine the probability of Steve being either a farmer or a librarian, based on limited information about his personality.

The participants were provided with the following information:

Steve is a quiet and shy individual who likes to read books and is not very social.

Based on this information alone, most participants concluded that Steve was more likely to be a librarian than a farmer. However, Kahneman and Tversky showed that this conclusion was not necessarily justified.

To demonstrate this, they presented participants with additional information that was relevant but not included in the initial description.

For example, they added information about the number of farmers relative to librarians and the percentage of farmers with Steve’s personality type still resulted in a higher number of farmers than the total number of librarians.

For instance, if there are 20x more farmers than librarians and 20% of farmers fit that personality type, it is still 4x (20 * 0.20) more likely that Steve is a farmer than a librarian.

When participants were given this new information, their probabilities for Steve being a farmer increased significantly, indicating that their initial conclusions were not sufficiently informed.

This study highlights the importance of stress-testing assumptions when making decisions based on limited information.

It is important to consider all relevant factors and not rely solely on initial assumptions or heuristics, such as stereotyping, when making decisions or forming judgments.

This approach is consistent with the Bayesian approach to probability, which involves continuously updating beliefs based on new information.

In trading and investing, it’s always important to ask how do you know that you know?

Correlation and Covariance

Correlation and covariance are two statistical concepts commonly used in probability theory to describe the relationship between two random variables.

Covariance measures how much two random variables change together, while correlation measures the strength and direction of their relationship.

A positive covariance indicates that the two variables tend to move in the same direction, while a negative covariance indicates that they tend to move in opposite directions.

A correlation coefficient ranges from -1 to 1, with values of 1 indicating a perfect positive correlation, values of -1 indicating a perfect negative correlation, and values of 0 indicating no correlation.

In trading/investing, correlation and covariance are useful tools for risk management and portfolio diversification.

By understanding the relationship between different assets, investors can better manage their portfolios by selecting assets that are not highly correlated with each other.

This can help to reduce overall portfolio risk by spreading investments across different asset classes and sectors.

For example, a portfolio of stocks that are all highly correlated with each other may be riskier than a portfolio of stocks or other assets that have lower correlations with each other.

By selecting a diverse range of assets with low correlations, an investor can create a more resilient portfolio that is less likely to suffer large losses during market downturns.

Additionally, understanding correlation and covariance can help investors to identify patterns in the market and predict future trends.

It’s also important to understand that correlations are backward-looking and tend to change over time.

For example, stocks and bonds may be negatively correlated in an environment where changes in discounted inflation fall, but may positively correlate in environments where discounted inflation rises.

So more robust interpretations of inflation will look more closely at what assets are like intrinsically based on the cause-effect economic linkages rather than backward-looking interpretations like simple correlation coefficients, which are merely fleeting byproducts of the environment they’re in.

FAQs – Probability Theory in Trading

What is the probability theory and why is it important in trading?

There are several important probability concepts that traders should understand.

Here are a few key ones:

• Probability Distributions: Probability distributions describe the likelihood of different outcomes in a random event. Traders use probability distributions to understand the potential range of outcomes for a given trade. Common probability distributions used in trading include the normal distribution, which describes the behavior of many financial variables, and the binomial distribution, which is used for modeling binary outcomes.
• Expected Value: The expected value of a trade is the average profit or loss that can be expected over the long term. By calculating the expected value, traders can assess the potential profitability of a trade and make more informed decisions about whether to enter or exit the trade.
• Standard Deviation: Standard deviation is a measure of the amount of variation or volatility in a set of data. Traders use standard deviation to understand the level of risk associated with a given trade. Higher levels of standard deviation indicate higher levels of risk. Note that standard deviation is based on the normal distribution, which is not a good fit for many financial asset/variable outcomes.
• Fat Tails: Events that appear more frequently than predicted by the normal distribution, indicating the potential for extreme price movements.
• Correlation: Correlation measures the strength and direction of the relationship between two variables. In trading, traders use correlation to understand how different assets move in relation to each other. A high positive correlation between two assets indicates that they tend to move in the same direction, while a negative correlation indicates they tend to move in opposite directions.
• Statistical Significance: Statistical significance refers to the likelihood that an observed result is not due to chance. Traders use statistical significance to evaluate the effectiveness of a trading strategy or to determine whether a particular market event is likely to have a meaningful impact on the market.
• Conditional Probability: The probability of an event occurring given that another event has already occurred.
• Bayesian Probability: A method of probability interpretation that updates the probability estimate for an event as new evidence or information becomes available.
• Random Walk Theory: The idea that security/asset price changes have the same distribution and are independent of each other, suggesting it’s impossible to predict future price movements based on past prices.
• Law of Large Numbers: A principle that states that as the number of trials or observations increases, the actual outcome will converge to the expected outcome.
• Monte Carlo Simulation: A computational technique that uses random sampling to obtain numerical results for problems that might be deterministic in principle.

Understanding these and other probability concepts can help traders make better decisions in markets and manage their risk more effectively.

Conclusion – Probability Theory in Trading

Probability theory plays a crucial role in trading as it helps traders make informed decisions based on data-driven analysis.

By using probability theory, traders can estimate the likelihood of potential market movements and develop trading strategies to capitalize on these movements.

It helps traders to assess the risk-reward ratio of a trade, manage their portfolio and optimize their positions.

Probability theory is particularly useful in quantifying uncertainty and measuring market volatility, enabling traders to anticipate and prepare for changes in the market.

Overall, probability theory provides traders with the tools to make more informed and accurate trading decisions, which can lead to improved profitability and reduced risk.