Importance of Expected Value in Trading

Every decision that you make in the financial markets should be formulated as an expected value calculation.
Every trade or every bet can be thought of as a probability. There is a probability and reward for being right and there’s a probability and penalty for being incorrect.
In other words, how to calculate expected value can be explained as:
Expected value = P(right) * R(right) – P(wrong) * R(wrong)
P = probability
R = reward
Typically, a winning trade will have a positive expected value – i.e., the value of the probability of being right multiplied by the reward for being right exceeds the probability of being wrong multiplied by the reward for being wrong. And a losing trade will have a negative expected value.
Traders want to maximize their expected value.
Key Takeaways – Expected Value
Expected value is a statistical concept that can be applied to trading. Here are three key takeaway points to explain the concept:
- Expected value is the average outcome of a trading strategy over many trades. It takes into account the probability of each outcome and the magnitude of the outcome, positive or negative.
- A positive expected value indicates that a trading strategy is expected to make money over the long run, while a negative expected value indicates that a trading strategy is expected to lose money over the long run.
- By calculating the expected value of a trading strategy, traders can assess whether the strategy is likely to be profitable or not, and make informed decisions about risk management and position sizing. However, it’s important to note that expected value is not a guarantee of future results and actual trading outcomes may differ from the expected value.
Expected Value Examples
Let’s look at some sample exercises.
Example #1
Suppose that the probability of being right is 70 percent and the reward for being right is $50, and the probability of being wrong is 30 percent and the reward for being wrong is $100 (or -$100 to denote the loss of money).
Is it smart to take this bet?
Following the formula:
EV = 0.70 * $50 + 0.30 * -$100 = $35 – $30 = +$5
Given the expected value is positive – if you have assessed your probabilities correctly – the expected reward is higher than the expected penalty. This could be a viable bet as long as you can cover the loss (-$100) in the event that you’re wrong.
Example #2
Understanding expected value, you can also observe that it doesn’t make sense to only bet on what’s most probable.
For example, in the markets, you will often be confronted with situations where your probability of being right is quite high, but the reward is low and the penalty for being wrong is correspondingly high.
Selling out-of-the-money (OTM) uncovered options is a common example. Many will sell OTM options believing that their chances of being right are high and this makes the bet favorable.
However, the actual profit/loss math is often quite a bit different.
If you have a 90 percent chance of being right and your reward is $20, but you have a 10 percent of being wrong and the penalty is $1,000, then reality can look a bit different:
EV = 0.90 * $20 + .10 * $1,000 = -$80
In this case, you might have a high win percentage, but if you’re not making positive expected value bets, you will lose money. And if you can’t cover the expected loss there’s the “risk of ruin” element.
When people wipe out their trading accounts it’s usually due to either excessive leverage, putting too much on any given bet in an all-or-nothing style (e.g., options, binary options), or by selling options.
Risk management is critical in any circumstance.
Example #3
On the other hand, if your odds of being right are low but the upside is high, and your odds of being wrong are high but the cost to being wrong is negligible, it could make sense to do it.
Let’s say you have a 99% chance of being wrong but your cost of being wrong is $100, and you have a 1% chance of being right but your reward is $100,000.
This could be a bet in the financial markets or it could be like sending out an additional job application and potentially going through the interview process that takes little time or lost opportunity elsewhere, but carries a tangible reward if you are successful in the form of a quality salary, benefits, and other perks.
EV = .01 * $100,000 + .99 * -$100 = +$901
Your reward is 1,000x the amount it costs if you are wrong or unsuccessful and you deem your odds as such that it makes sense to give it a shot even if the odds are seemingly overwhelmingly against you.
If you can afford the cost to being wrong and you have accurately assessed your odds, then the decision is very reasonable.
In trading, the concept is similar. If you are making positive expected value bets repeatedly, you will generate profitable results over time.
Some strategies that focus on tail events can be wildly profitable rarely (e.g., 2008 financial crisis) and only lose a little bit in most other environments.
Mark Spitznagel, the head of Universa Investments, captured the idea:
“When the market crashes, I want to make a whole lot, and when the market doesn’t crash, I want to lose a teeny, teeny amount. I want that asymmetry… that convexity.”
If you are losing money and doing so over a sample size that makes it likely you’re not simply dealing with the vagaries of the market, then you need to really assess whether the strategy (or strategies) you are using is putting the odds in your favor.
It’s important to resist the temptation that losing money means that you simply don’t have luck on your side.
Example #4
If you were playing a coin-flipping game where you could bet on either heads or tails, each had an equal chance of turning out correctly, would you risk $100 to make $199 if you were to be right ($100 initial bet is returned plus $99 on top of that) and lose the entire $100 if you’re wrong?
Following the formula:
EV = 0.50 * $99 + 0.5 * -$100 = -$0.50
So, the answer should be no.
The expected value is only slightly negative, so your margin doesn’t look bad.
However, if you played this game 200 times with an equal $100 bet each time, you would expect to lose $100 (200 multiplied by the expected loss of -$0.50), or equal to your regular bet size.
Nonetheless, there is still a 36.7% chance* that you would actually be profitable after 200 rounds of this game. (It would take 919 rounds before your chances of being profitable dipped to less than 1%.)
* This is figured by taking the expected payoff per bet, taking the difference relative the amount wagered per bet, and dividing by the amount wagered per bet. Then taking it to the power of however many rounds were played:
[($100 + -$0.50) / $100]^200 = ($99.5/$100)^200 = .995^200 = .367 = 36.7%
It could take a while to learn that you actually have a bad strategy if you are right on the border between something that’s viable and not any better than flipping a coin.
Example #5 – American Roulette
On an American roulette wheel, there are 38 numbers, 18 red, 18 black, and 2 green.
If you bet $10 on red 10 different times, what would be your odds of making money?
If you get it right, you get $20 (double your bet size), while if you get it wrong, you lose everything.
There are 18 red pockets and 38 total pockets, so your expected value per round would be:
EV = 18/38 * $20 + 20/38 * $-10 = $9.47
This would represent an expected loss of $0.53 per round ($10 minus the expected value).
Odds of losing money after 10 rounds?
The probability of losing money after 10 rounds, assuming you make even-money bets each round, can be calculated using the binomial distribution, which is a mathematical formula that describes the probability of a certain number of successes in a fixed number of trials.
Assuming you start with a certain amount of money and want to know the probability that you will end up with less than that amount after 10 rounds of even-money betting, the probability of losing money can be calculated as follows:
P(loss) = Σ (i = 0 to 10) (10 choose i) * (47.37%)^i * (52.63%)^(10-i)
Where “i” represents the number of rounds you win, “10 choose i” represents the number of ways to choose “i” winning rounds out of 10, and (47.37%)^i and (52.63%)^(10-i) represent the probability of winning “i” rounds and losing (10-i) rounds, respectively.
Using a calculator or statistical software, this equation can be evaluated to find that the probability of losing money after 10 rounds of even-money betting on American roulette is approximately 87.9%.
Therefore, the odds of losing money after 10 rounds of equal-betting each round on American roulette are quite high.
Odds of losing money after 100 rounds?
If you continue to make even-money bets for 100 rounds of American roulette, the probability of losing money can be calculated in a similar manner using the binomial distribution.
The probability of losing money after 100 rounds can be calculated as follows:
P(loss) = Σ (i = 0 to 100) (100 choose i) * (47.37%)^i * (52.63%)^(100-i)
Using a calculator or statistical software, this equation can be evaluated to find that the probability of losing money after 100 rounds of even-money betting on American roulette is approximately 99.8%.
Example #6 – European Roulette
European roulette is similar to American roulette, but with one key difference: it only has a single 0 pocket, while American roulette has both 0 and 00 pockets. This means that the odds of winning an even-money bet on European roulette are slightly better than on American roulette, since there is one less pocket that gives the house an edge.
Assuming you make even-money bets (e.g. betting on red or black, odd or even, high or low), the odds of winning an individual bet on European roulette are 18/37, or approximately 48.65%. The odds of losing an individual bet are therefore approximately 51.35%.
So your EV when betting on red or black is:
EV = 18/37 * $20 + 19/37 * $-10 = $9.73
So you’d expect to lose $0.27 per round.
Your odds of making money over 10 tries is:
1 – ($9.73/$10)^10 = 1 – 0.973^10 = 1 – 0.58 = 0.42 = 42%
To calculate the probability of losing money after a certain number of rounds of equal-betting each round, we can use the same binomial distribution formula as we did for American roulette.
Assuming 10 rounds of even-money betting on European roulette, the probability of losing money can be calculated as follows:
P(loss) = Σ (i = 0 to 10) (10 choose i) * (48.65%)^i * (51.35%)^(10-i)
Using a calculator or statistical software, this equation can be evaluated to find that the probability of losing money after 10 rounds of even-money betting on European roulette is approximately 83.22%.
If we assume 100 rounds of even-money betting on European roulette, the probability of losing money can be calculated as follows:
P(loss) = Σ (i = 0 to 100) (100 choose i) * (48.65%)^i * (51.35%)^(100-i)
Using a calculator or statistical software, this equation can be evaluated to find that the probability of losing money after 100 rounds of even-money betting on European roulette is approximately 94.40%.
Therefore, the odds of losing money after 100 rounds of equal-betting each round on European roulette are still quite high, but slightly lower than the odds of losing money on American roulette.
Takeaways
Here are some key takeaways:
Expected Value Reflects Average Outcomes, Not Guarantees
Expected value helps understand whether a decision has a positive or negative average return over time, but it doesn’t predict exact results for each instance.
For example, in Example #1, the EV is positive, suggesting the bet is worth considering, assuming you can afford potential losses.
High Probability Doesn’t Mean Positive Expected Value
A high probability of winning isn’t enough if the reward is too small or the loss too large.
In Example #2, a 90% chance of winning with a small gain versus a 10% chance of a big loss leads to a negative EV, which would drain funds over time.
Asymmetric Payoffs with Low Probabilities Can Be Worthwhile
Sometimes, a bet with a low probability of success can have a positive EV if the potential gain is high relative to the potential loss.
Example #3 shows that with a 1% chance to win $100,000 versus a 99% chance to lose $100, a low-probability outcome may still make sense due to the favorable payoff ratio.
Marginally Negative EV May Not Be Obvious Immediately
In games with near-break-even outcomes, like the coin flip in Example #4, you may not notice the downside until many rounds.
Small negative EVs accumulate into significant losses over time.
This illustrates why seemingly harmless choices can add up negatively.
It’s not unlike blackjack in a casino where the “house” has a 1-2% edge and over the long-run people lose money.
It can even apply to daily habits, such as how eating poorly can lead to negative health outcomes over time.
Probability of Losing Over Time is Key in Games with Negative EV
For games with a known negative EV, like Examples #5 and #6 (American and European roulette), the probability of losing money increases sharply with repeated rounds.
The longer you play, the higher the chance of an overall loss, demonstrating the importance of not overestimating short-term wins.
Risk Management and Capital Reserves Matter
Even with a positive EV, you must manage risk to avoid the “risk of ruin.”
For instance, Example #1 is only viable if you can withstand a $100 loss.
Not having enough capital or risking too much on each bet can lead to ruin despite a favorable EV.
Skewness and Tailedness Influence Strategy
Strategies that target tail events (rare, high-impact outcomes) can generate profits, but typically involve small losses in other scenarios.
Example #3 shows how a small chance of a massive gain can justify the bet.
Strategies like these, known as “convex” strategies, seek outsized rewards when the unlikely does happen.
For traders, just because something is 60/40 doesn’t mean you should necessarily position for the 60.
Expected value should guide decisions alongside skew, tailedness, and other factors related to the nature of the distribution, correlations, interdependencies, risk, and other second-/nth-order effects.
With this, you can build a sustainable approach to decision-making.
Is It Always Best to Focus Only on Expected Value?
No, making a positive expected value trade or decision (or the highest EV trade or decision) is not always the best choice.
Here are a few reasons why:
Risk Management
A positive expected value trade or decision may still carry significant risk.
Traders need to consider not only the expected value of a trade but also the potential downside risk, including the possibility of a significant loss.
Risk management is an important part of any trading strategy, and traders must be able to identify and manage risk to minimize potential losses.
If you have a known 51/49 edge on something and you can bet $10 on that over and over again, you’ll do that forever if you can. However, you don’t want to commit a significant amount of money to it because you can lose many 51/49 situations in a row.
Opportunity Cost
Even if a trade has a positive expected value, it may not be the best use of a trader’s capital.
If there are other trading opportunities that offer a better risk-to-reward ratio or higher potential profits, a trader may choose to pursue those opportunities instead of the positive expected value trade.
Lower EV Situations With Lower Variance
Let’s say you’re playing a game with three options:
- Option 1: 80% chance of winning $10,000
- Option 2: 20% chance of winning $100,000
- Option 3: 5% chance of winning $1,000,000
Your expected values in each situation are:
- $8,000
- $20,000
- $50,000
What would most people choose in this situation?
What most people would choose in this situation depends on a variety of factors, including their risk tolerance, financial situation, and overall goals.
Here are a few possible scenarios:
- High-Risk, High-Reward: Some people may be willing to take on more risk in exchange for a chance at a high reward. For these individuals, option 3 (5% chance of winning $1,000,000) may be the most appealing, despite the lower expected chance of winning. They may be willing to accept lower odds in exchange for a small chance at a very large payout and the highest expected value option.
- Moderate Risk, Moderate Reward: Others may be more risk-averse and prefer to take a more moderate approach. In this case, option 2 (20% chance of winning $100,000) may be more appealing. While the expected value is lower than option 3, the probability of winning is higher, making it a more moderate risk-reward option.
- Low Risk, Low Reward: For those who are highly risk-averse or have limited financial resources, option 1 (80% chance of winning $10,000) may be the most appealing. While the expected value is lower than options 2 and 3, the probability of winning is much higher, making it a safer option with a more modest reward.
In the markets, this might be analogous to choosing between safe bonds, equities, or speculative startup investments.
Probabilities Are Dynamic and Often Unkown
Probabilities are often not known explicitly and they are rarely static.
The market can be unpredictable, and factors such as unexpected news events or changes in market sentiment can quickly change the expected value of a trade.
Traders must be able to adapt to changing market conditions and adjust their strategies accordingly.
Trading Costs
Making a positive expected value trade does not guarantee a profit, as trading costs such as commissions, fees, and spreads can eat into potential profits.
Traders must take these costs into account when calculating the expected value of a trade and adjust their strategies accordingly.
In sum, while positive expected value trades or decisions are generally preferred, traders must consider other factors such as risk management, opportunity cost, market conditions, and trading costs when making decisions. Trading is a complex and dynamic process, and traders must be able to adapt to changing market conditions and make informed decisions based on a variety of factors.
Expected Value in Options Trading
Expected value comes up quite a bit in options trading, in particular.
Many traders like options because it enables them to capture a specific part of the distribution of potential outcomes. That means they can more carefully tailor trading ideas and investment theses to express certain viewpoints.
To understand whether a trade is worth putting on, running some expected value calculations is important.
You will have potential outcomes that you know beforehand based on how you structure the trade.
Then you will have to assign probabilities to each outcome to determine the expected value from each component. Adding them all up will give the expected value for the entire trade.
Example
Let’s say you wanted to put on a covered call on a stock, taking the nearest expiries one week out. To be safe, you also wanted to limit your losses in case share prices fall, so you also buy put options.
Let’s say the shares trade for $54 each. Assume you want to buy 1,000 shares.
You wanted to maximize the volatility risk premium you get out of the market, so you sell call options with a 54 strike.
To be defensive in case shares drop, you also buy put options with a 52 strike. This limits your potential losses to $2 per share.
Your trade structure is essentially a type of collar that looks something like the diagram below with a breakeven point that will come somewhere in the middle.
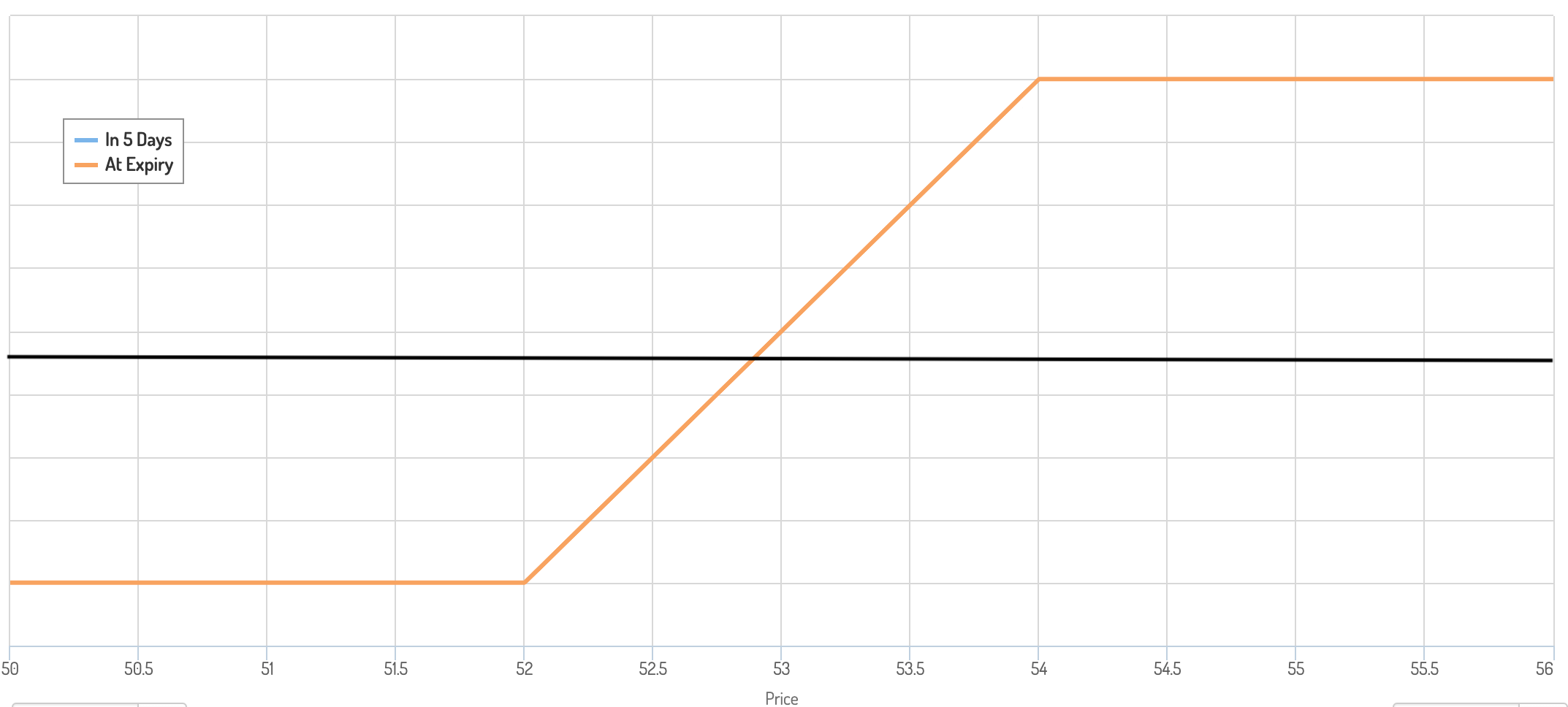
Potential outcomes
You have three categorical outcomes in terms of the end result:
- Trades above the upper bound of the collar (i.e., above $54 per share)
- Trades within the collar (i.e., between $52 and $54 per share)
- Trades below the lower bound of the collar (i.e., below $52 per share)
Since the upper bound of the collar is where price is trading currently, being above the upper bound of the band is the most likely of these three scenarios.
It’s on a weekly timeframe, so your odds of finishing above the band are about 50 percent.
We can also say that trading within the collar (0-3.7 percent out-of-the-money (OTM)) has about a 33 percent chance based on what’s implied by the options pricing.
Certain brokers (e.g., Interactive Brokers with their ‘Probability Lab’ feature) have these tools available to you.
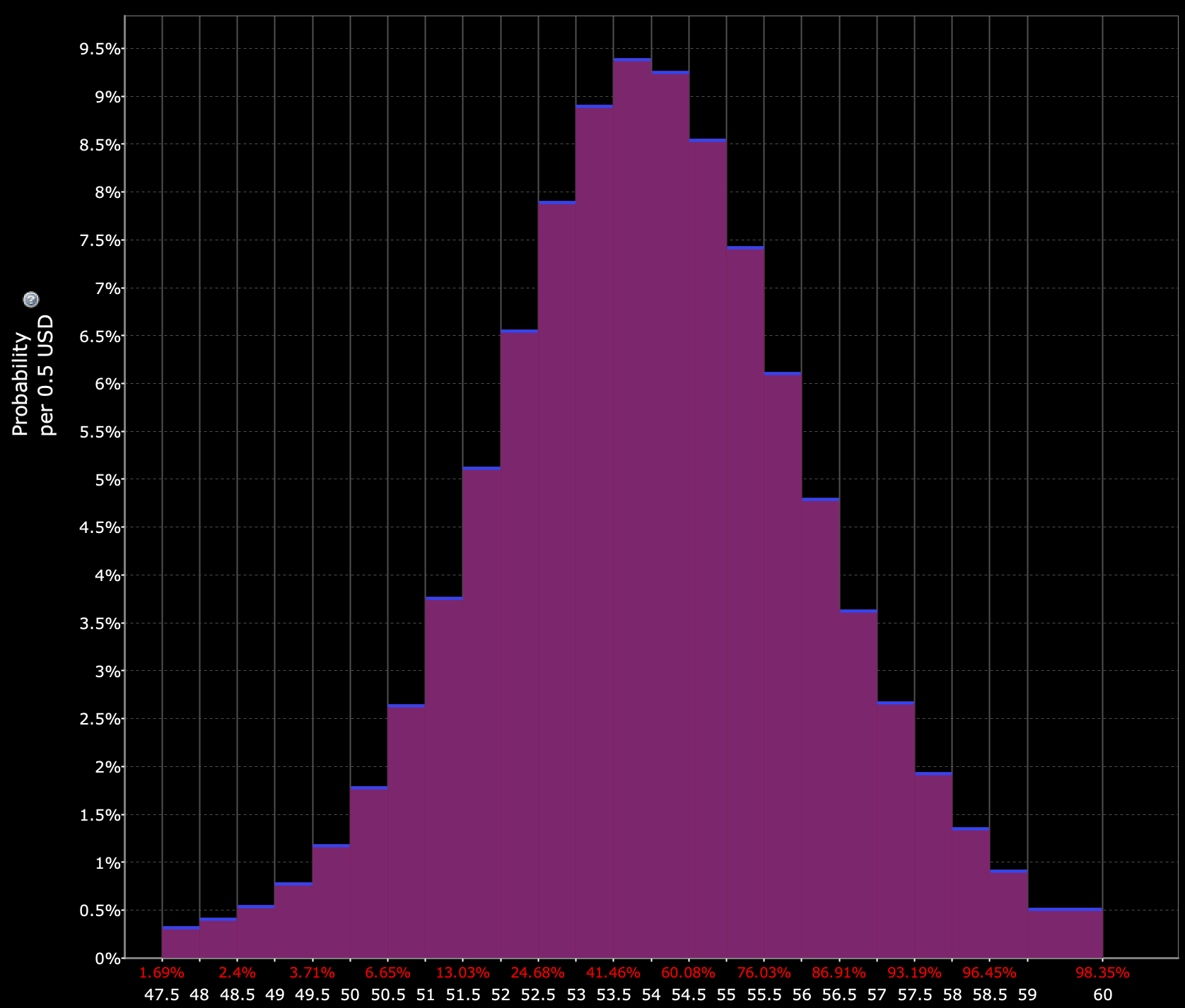
(Source: Interactive Brokers)
That means trading below the lower bound of the collar ($52 on down) has about a 17 percent chance.
How to calculate the expected value of this trade structure
To tabulate the expected values associated with “above upper bound” and “below lower bound” scenarios, we simply take the cost of the options and relevant movement in the stock.
To determine the expected value of the middle category, we can simply take the price midpoint and go based on that (in this case $53 per share).
‘Above upper bound’ gain/loss
For the “above upper bound” the expected value is simply the credit we get from selling the 54 calls.
Since we bought 1,000 shares and there are 100 shares per option contract, that’s 10 contracts. They were selling for $94 per contract ($0.94 per share), so that’s $940 total.
The cost of the 52 puts was $29 per contract ($0.29 per share), so that $290 total.
We subtract the two, $940 minus $290, which is +$650.
‘Below lower bound’ gain/loss
In this case, we still get the $650 net profit from the options.
However, if we go below $54 we suffer capital losses on the shares. Being long the 52 puts caps the losses at $2 per share ($54 minus $52). At 1,000 shares, that $2,000.
So, we gain $650 from in profit minus $2,000, for a loss of $1,350.
‘Within the collar’ gain/loss
In this case, we’re taking the midpoint ($53 by expiration).
Here we have a $1 capital loss per share. With 1,000 shares, that’s $1,000.
We gain $650 from the net profit from the options and subtract the $1,000 (the loss), for a net loss of $350.
What’s our expected value?
We multiply our individual gain/loss by the probability of it occurring.
So we get:
- Above upper bound: $650 * 0.50 = $325.00
- Below upper bound: -$1,350 * 0.17 = -$229.50
- Within collar: -$350 * 0.33 = -$115.50
We sum these values and get minus-$20 for an expected value.
So, if we assessed our probabilities as such, we would not have a positive expected value.
It would make sense for this figure to be about breakeven because we are largely using approximate market-implied probabilities.
This illustrates another reality that to make money in the markets (in excess of a benchmark) you need to bet against the consensus and be right.
If we believed our probabilities associated with each were more like 0.52, 0.15, and 0.33, then our expected value would be positive-$20.
Other factors in expected value calculations
Transaction costs are especially important to include.
This is not only the cost of the trade, it’s also the spread in what you’re trading and the quality of the execution.
It also includes financing costs and/or borrow fees.
Many securities and markets don’t have very liquid options markets, meaning the spread is often quite wide and there’s a lack of size at the bid and ask price.
This is especially important for large institutions and larger accounts, in general. Transaction costs tend to increase in a non-linear way.
Transaction costs may also influence what you want to trade.
For example, if you trade mid- to long-duration bonds, ZB futures include $150k to $200k worth of bonds per one contract, depending on the exact price. That means you can buy just one option contract for ZB futures versus having to buy around 11 contracts for an equivalent amount of TLT (a longer-duration bond ETF equivalent).
Brokers often charge based on the volume of contracts. Futures options prices are generally more expensive than stock and ETF options prices. But futures generally include a larger volume of the underlying per contract, which can help you cut some expenses if the size is appropriate for your portfolio.
Going from the intuitive to the explicit
Even if you don’t consciously make expected value calculations, you do them all the time intuitively.
If you have a flight to catch, you’re likely to leave for the airport well ahead of time to give yourself a reasonable time cushion.
This way you make it nearly impossible for you to miss your flight in case you have an issue with traveling to the airport, long lines, a security holdup, a misplaced ticket or passport, or whatever else could cut into that time buffer.
You do this because the downside to missing a flight is high in terms of monetary cost, inconvenience, and/or lost opportunity.
Choosing to not speed in your car is another form of an expected value calculation. While your odds of receiving a ticket for speeding are fairly low if you’re barely going over the speed limit, you might choose to not consciously speed at all if the downside risk of receiving a traffic violation is unacceptably high (i.e., a monetary fine, lost time getting pulled over, and perhaps more).
Trading is no different than the real-life scenarios we face and make to maximize our utility and limit our risk.
Taking a shot when you have a lot to gain and very little to lose (e.g., job opportunities) is a lot like trading situations where you have limited downside and theoretically unlimited upside (e.g., buying cheap OTM options).
Likewise, it’s best to take proper caution when your downside is very large even if you perceive the odds to be low (e.g., a doctor’s checkup if you’re experiencing a certain symptom). This is similar to traders selling out-of-the-money (OTM) options for very little premium.
When the low probability event does happen, they lose many multiples of whatever premium they planned on receiving (sometimes hundreds or worse).
As traders grow in experience and wisdom, they are less eager and less likely to trade things they don’t have strong conviction over.
Ironically, novice traders tend to be fairly confident and willing to dive in, while experienced traders tend to be the most afraid of being wrong based on their exposure to markets over time and the inevitable painful spells that has likely produced.
All traders should go into a trade with an explicit understanding of how bad things can get and how much upside they have. This is why some traders choose to never be short gamma (which basically means they never sell options).
While this philosophy will cause some to never take advantage of a source of return known as the volatility risk premium, they know that if they’re never short gamma they can never blow up. For some, it’s a matter of prudent risk management.
Traders tend to use the recent past to inform the future. Things can unfold that aren’t in your distribution and can’t be priced.
If something has never happened before, then the only way to hedge against the unknown is to cut off the tail risk entirely. Accordingly, many traders who are very advanced in understanding risk and reward will try to structure their trades using options.
If they do sell options, they are covered through a position in the underlying or through a different leg of the options structure. Buying options puts risk management entirely on the shoulders of the counterparty (i.e., the person who sold it to you).
It also eases the ability to make expected value calculations given you have a clearly defined downside.
Moreover, for those who set stop-losses, markets will gap when they close down to active trading for some period or when there’s a dislocation or big news event or piece of data. A stop-loss will not mitigate risk during abnormal periods.
Conclusion
If you are a trader or a professional gambler or any type of professional decision-maker, it’s critical that you know the concept of expected value.
Markets are similar to poker. You have to constantly assess your odds of being right, what your reward is for being right, the odds and penalty of being wrong, and how to assess this information with knowledge that is almost always imperfect.
Making the best trading decisions requires a strong understanding of risk and reward.
What is your downside, how much can you make on the upside, and, very importantly, what are the probabilities of those things happening?
It’s not an easy process. For different traders it means different things.
Some traders want to explicitly know what their downside is by being long options or by having strict risk management in the form of a stop-loss.
They know two types of risk are under control: (1) how much they can lose and (2) that the “risk of ruin” is impossible (they can always cover the loss).
The best traders keep losses minimal when they’re wrong and make healthy profits when they’re right.
To use a baseball analogy, it’s not your batting average that matters (ratio of successful at-bats to total at-bats), it’s your slugging percentage (the overall quality of the at-bats or how much is produced when you are successful).
Betting on what’s most probable is not always the best thing to do when traders understand expected value.
Too many target “easy wins” – e.g., selling OTM options – and end up wiping out the benefit of a bunch of tiny-profit wins with what happens when inevitably one of those goes against them, and often by several multiples.
In Short
Expected value is a crucial element of any speculative pursuit. It should form the basis of any risk based trade.
How To Calculate Expected Value
Expected value = P(right) * R(right) – P(wrong) * R(wrong)
- P = probability
- R = reward