Measure Theory in Finance & Trading

Measure theory is a branch of mathematics that studies ways of generalizing the notion of integration, length, area, and volume.

It’s used in probability theory, and by extension, it is fundamentally important in the fields of finance and trading, which is essentially an applied probability exercise.

In these areas, measure theory underpins the mathematical models used to price financial instruments, manage risk, and develop trading strategies.

Key Takeaways – Measure Theory in Finance & Trading

• Quantifies Uncertainty
  • Measure theory provides a mathematical framework to quantify and manage unknowns in financial markets.
  • Traders can assess probabilities of various outcomes.
• Foundation for Modern Finance
  • It underpins modern financial theories, including risk management and derivative pricing, by allowing for the calculation of integrals and probabilities over complex financial instruments.
• Improves Risk Assessment
  • By applying measure theory, traders can more accurately model the risk and return of securities.
  • Enhances portfolio optimization and the valuation of derivatives through more sophisticated probabilistic analysis.

Measure Theory Applications in Finance and Trading

Risk Management

Measure theory is essential for quantifying risks in financial markets.

The concept of a measure allows for the calculation of probabilities of various outcomes, including extreme events.

This is particularly important in Value at Risk (VaR) calculations and for tail risk management in portfolios.

Option Pricing Models

The famous Black-Scholes model and other option pricing models rely on measure theory.

Specifically, the change of measure (Girsanov’s theorem) allows for the pricing of derivatives under the risk-neutral measure.

Under the risk-neutral measure, the expected return of the underlying asset is the risk-free rate, which facilitates the calculation of the present value of expected payoffs.

Stochastic Processes

Measure theory provides the foundation for understanding stochastic processes, which model the random evolution of prices over time.

It’s essential for the proper definition and analysis of continuous-time processes like Brownian motion and martingales.

These are used in financial mathematics for modeling price dynamics and for arbitrage pricing theory.

Portfolio Optimization

In optimizing portfolios, measure theory is used to model the return distributions of assets.

This allows for the calculation of expected returns, variances, and covariances under various measures.

These are important for constructing efficient portfolios under the mean-variance optimization framework or more advanced risk measures like CVaR (Conditional Value at Risk).

How Traders Can Use Measure Theory

Quantitative Trading Strategies

Traders can apply measure theory in the development of algorithmic trading strategies that are based on probabilistic models of price movements.

By understanding the underlying measures, traders can better assess the likelihood of certain economic/market conditions and use that to refine their strategies.

Risk-Adjusted Returns

Measure theory enables traders to compute and analyze risk-adjusted returns more accurately.

By understanding the distribution of returns under different measures, traders can make better decisions that account for the risk of their investments/positions/return streams.

Tail Risk Hedging

The application of measure theory allows traders to identify and hedge against tail risks – rare but catastrophic events that can lead to significant losses.

By analyzing the measure of the tails of return distributions, traders can implement strategies to protect their portfolios against extreme downside risk (e.g., better diversification, hedging, risk balancing).

Dynamic Hedging

For options traders, measure theory is key to dynamic hedging strategies, which involve continuously adjusting the positions in the underlying asset to hedge against the option’s price movements.

The theoretical framework provided by measure theory allows for the calculation of the hedge ratio (delta, most commonly, followed by gamma and there are other “Greeks“) under continuous-time modeling.

Coding Example – Measure Theory in Trading (Portfolio Optimization)

Applying measure theory to portfolio optimization involves quantifying and managing the probabilistic distributions of returns and risks.

In this simplified example, we’ll optimize a portfolio consisting of stocks, bonds, commodities, and gold – a portfolio we’ve used as an example in many other articles – based on their expected forward returns and annualized volatility, assuming uncorrelated returns for simplicity.

• Stocks: +3-8% forward return, 15% annualized volatility using standard deviation
• Bonds: +1-5% forward return, 10% annualized volatility using standard deviation
• Commodities: +0-4% forward return, 15% annualized volatility using standard deviation
• Gold: +1-6% forward return, 15% annualized volatility using standard deviation

We’ll use Python to calculate the optimal portfolio allocation that maximizes expected return for a given level of risk.

This example won’t go very far into measure theory mathematically but will demonstrate how to handle returns and volatilities in a portfolio context.

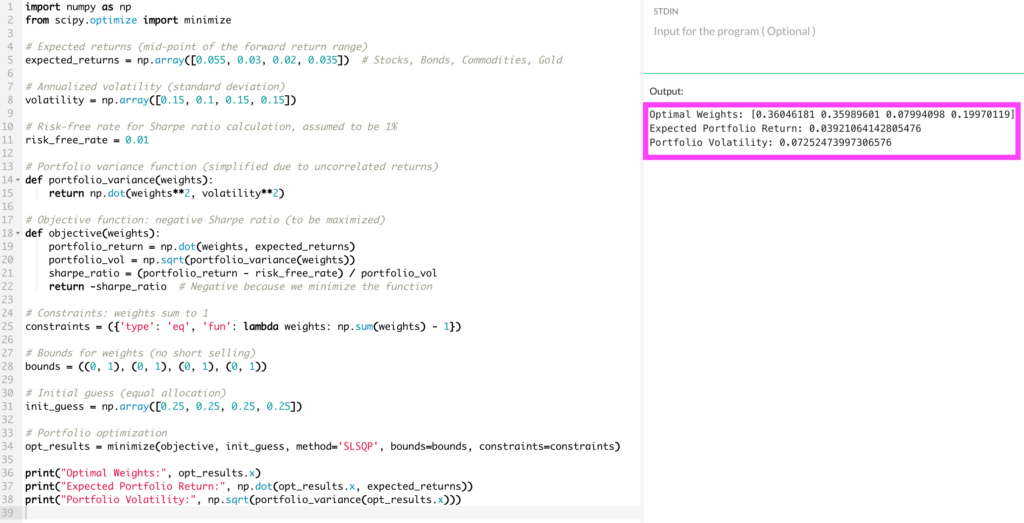
import numpy as np
from scipy.optimize import minimize

# Expected returns (mid-point of the forward return range)
expected_returns = np.array([0.055, 0.03, 0.02, 0.035]) # Stocks, Bonds, Commodities, Gold

# Annualized volatility (standard deviation)
volatility = np.array([0.15, 0.1, 0.15, 0.15])

# Risk-free rate for Sharpe ratio calculation, assumed to be 1%
risk_free_rate = 0.01

# Portfolio variance function (simplified due to uncorrelated returns)
def portfolio_variance(weights):
    return np.dot(weights**2, volatility**2)

# Objective function: negative Sharpe ratio (to be maximized)
def objective(weights):
    portfolio_return = np.dot(weights, expected_returns)
    portfolio_vol = np.sqrt(portfolio_variance(weights))
    sharpe_ratio = (portfolio_return - risk_free_rate) / portfolio_vol
    return -sharpe_ratio # Negative because we minimize the function

# Constraints: weights sum to 1
constraints = ({'type': 'eq', 'fun': lambda weights: np.sum(weights) - 1})

# Bounds for weights (no short selling)
bounds = ((0, 1), (0, 1), (0, 1), (0, 1))

# Initial guess (equal allocation)
init_guess = np.array([0.25, 0.25, 0.25, 0.25])

# Portfolio optimization
opt_results = minimize(objective, init_guess, method='SLSQP', bounds=bounds, constraints=constraints)

print("Optimal Weights:", opt_results.x)
print("Expected Portfolio Return:", np.dot(opt_results.x, expected_returns))
print("Portfolio Volatility:", np.sqrt(portfolio_variance(opt_results.x)))

Conclusion

Measure theory provides the mathematical underpinnings for risk management, derivative pricing, and portfolio optimization.

Its concepts allow traders and financial analysts to model and understand the complexities of financial markets in a mathematically rigorous way.

The practical application of measure theory in trading requires not only a strong mathematical background but also a thorough understanding of financial markets and instruments.