1. Home
2. Glossary

Delta

Written By

Dan Buckley

Written By

Dan Buckley

Dan Buckley is an US-based trader, consultant, and part-time writer with a background in macroeconomics and mathematical finance. He trades and writes about a variety of asset classes, including equities, fixed income, commodities, currencies, and interest rates. As a writer, his goal is to explain trading and finance concepts in levels of detail that could appeal to a range of audiences, from novice traders to those with more experienced backgrounds.

» Dan Buckley Profile Page

Updated

Jul 16, 2022

Delta (∆) measures the rate of change of an option’s value (V) with respect to the change in an underlying asset’s price (S).

∆ = ∂V/∂S

Delta is one of the first-order Greeks in finance and plays a crucial role in risk management.

Each Greek measures the sensitivity of the change in one parameter (e.g., value of a security) to a change in a different parameter, treating them in isolation.

This helps understand a portfolio’s exposures and what might need to be done to rebalance a portfolio to obtain a desired exposure.

Delta and other Greeks are commonly calculated using the Black-Scholes model. Delta is among the most useful for hedging purposes.

The most common type of rebalancing procedure based on usage of the Greeks is what’s called delta hedging.

Delta is commonly employed by market makers. If they sell an option, in order to reduce their exposure to the underlying value of the security, they will hedge by buying or selling the underlying asset to better neutralize their portfolio.

They typically manage this dynamically.

Example

Let’s say that a market maker wants to sell 10 SPY 400 calls.

In order to hedge the exposure to the underlying, they could look at the delta to help understand how many shares to buy.

Ten options contracts contain notional exposure of 1,000 shares. The 400 calls are out-of-the-money (OTM) so the delta is still quite some way’s from 1.00 (fully in-the-money (ITM)).

The delta of a certain option is typically listed within options chains

With a delta of 0.517, the market maker would go long 517 shares – i.e., 1,000 * 0.517.

Delta’s visibility within an options chain

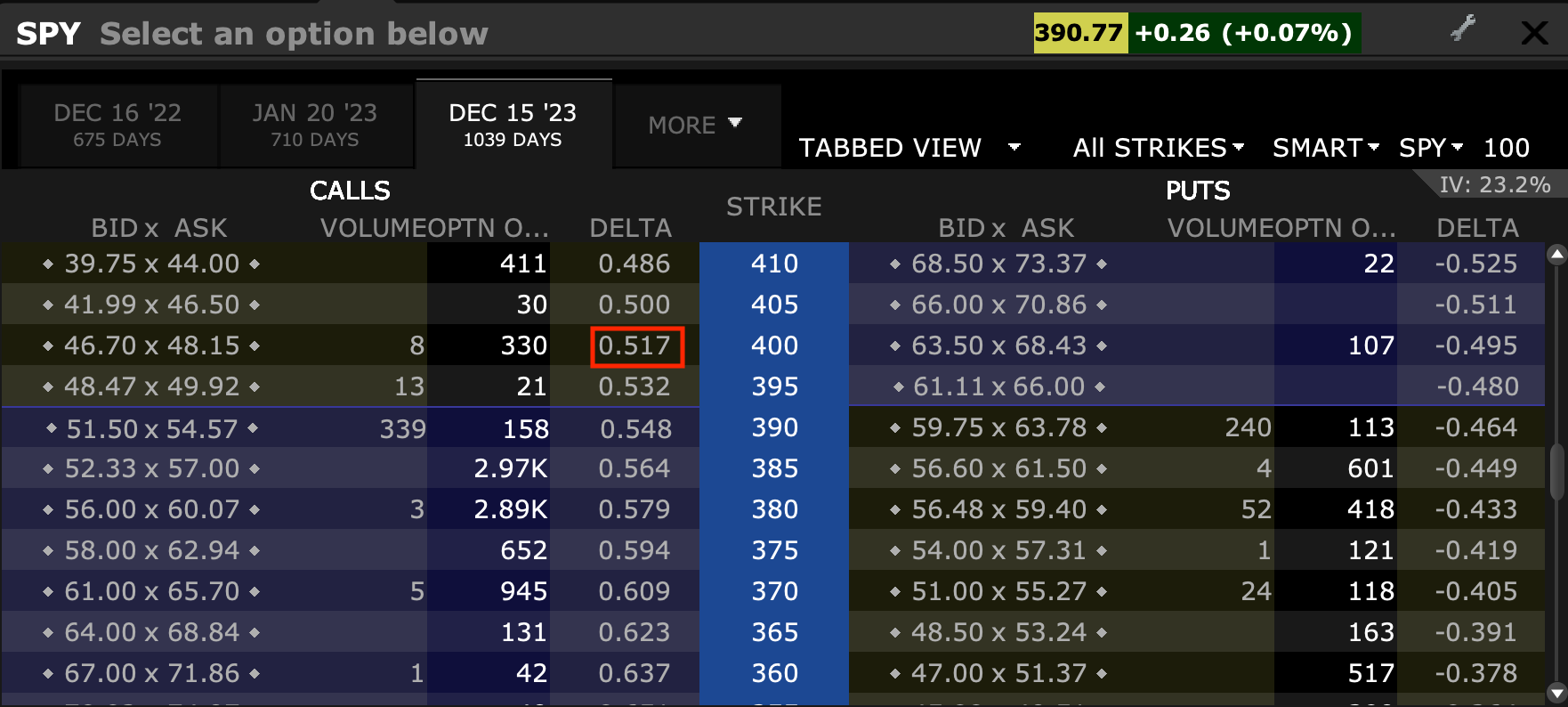
(Source: Interactive Brokers)

If the price of the underlying decreases, the delta would decrease, so the market maker might sell some shares.

If the price of the underlying increases, the delta would increase, so the market maker might buy some shares.

Note that for call options, the corresponding delta is positive, which denotes a positive change in the value of the underlying

For put options, the corresponding delta is negative to denote a negative change in the value of the underlying.

Uses of Delta

Delta is a number between 0.0 and 1.0 for a long call (or a short put) and between 0.0 and -1.0 for a long put (or a short call). This goes for standard vanilla options; for exotic options, it’s more complex.

When a call option is deep OTM, its delta will be around 0.0 to show that movements in the underlying don’t have much influence on its change in value.

This means that its probability of landing ITM – and therefore have a value above zero – is still small.

When a call option is deep ITM, its delta will be around 1.0 to basically approximate the movement of a certain quantity of the underlying (e.g., 100 shares if an equity option).

Something that’s around ATM will have a delta somewhere around 0.50.

At the same strike price, the difference between the delta of a call and delta of a put is close to being equal to one. They tend to differ slightly due to the spot price and forward price varying due to a discount factor.

Intuition of delta

The delta is an intuitively straightforward number because the option acts like the number of shares indicated by the figure.

For example, if a trader has a portfolio of 100 AAPL options with an average delta of 0.35, that’s the equivalent to 3,500 shares of Apple (100 options contracts * 100 shares per contract * 0.35).

So, the trader can expect the portfolio to act just like 3,500 shares (long) of Apple. While the notional value of 100 options is 10,000 shares, the delta indicates a set of options that are OTM on average. Therefore, they effectively act as a fraction of that price.

Each one percent increase in the underlying would increase the value of the options portfolio by 0.35 percent.

And as the price of the underlying increases, the delta of the option also increases. Its value starts increasing more rapidly. This is part of the convexity and intrinsic leverage associated with options.

This increases the sensitivity of the option’s price to changes in the underlying going forward, holding volatility (vega), time (theta), and rho (interest rates) constant (and other things, to a lesser extent, such as second- and third-order changes).

While put option deltas are negative, they often aren’t quoted as a negative number. It’s understood that a put option carries a bearish sensitivity toward the underlying and is therefore negative.

What traders care most about is the magnitude of the number.

Delta Linearity

Delta is a linear factor. This means that in order to find the delta of a portfolio, you can take the sums for each individual position.

If you own the underlying asset instead of a vanilla option, the delta of that position is always one – denoting that linear exposure.

Options, on the other hand, are more convex. You can make or lose a lot of money on the premium you pay.

Accordingly, if a trader needs to hedge, he can simply go long or short the number of shares necessary as indicated by the delta.

A delta of minus-0.40 on ten put options contracts (for stocks) means shorting 400 shares. If the delta goes to minus-0.38, he can buy 20 shares to rebalance the portfolio to being short 380 shares.

By doing so, the portfolio retains its total value irrespective of price movements in the underlying asset for smaller movements.

The wider the movements in price – holding any changes in volatility, time, and (usually to a lesser extent) in interest rates (rho) constant – the more delta will change.

Impact On Underlying Asset Market

This process of rebalancing equity exposure due to delta naturally has an effect on the underlying market for the asset.

If a trader owns 100 shares of a stock and wants to hedge his risk by buying an OTM put option with a delta of minus-0.15, that can effectively be the equivalent of shorting 15 shares of the stock.

The counterparty selling the trader the put option probably wants to hedge its exposure from the potential liability of the put option by selling shares short. (Or perhaps reducing a long position, depending on what its aggregate account looks like, but the effect is the same.)

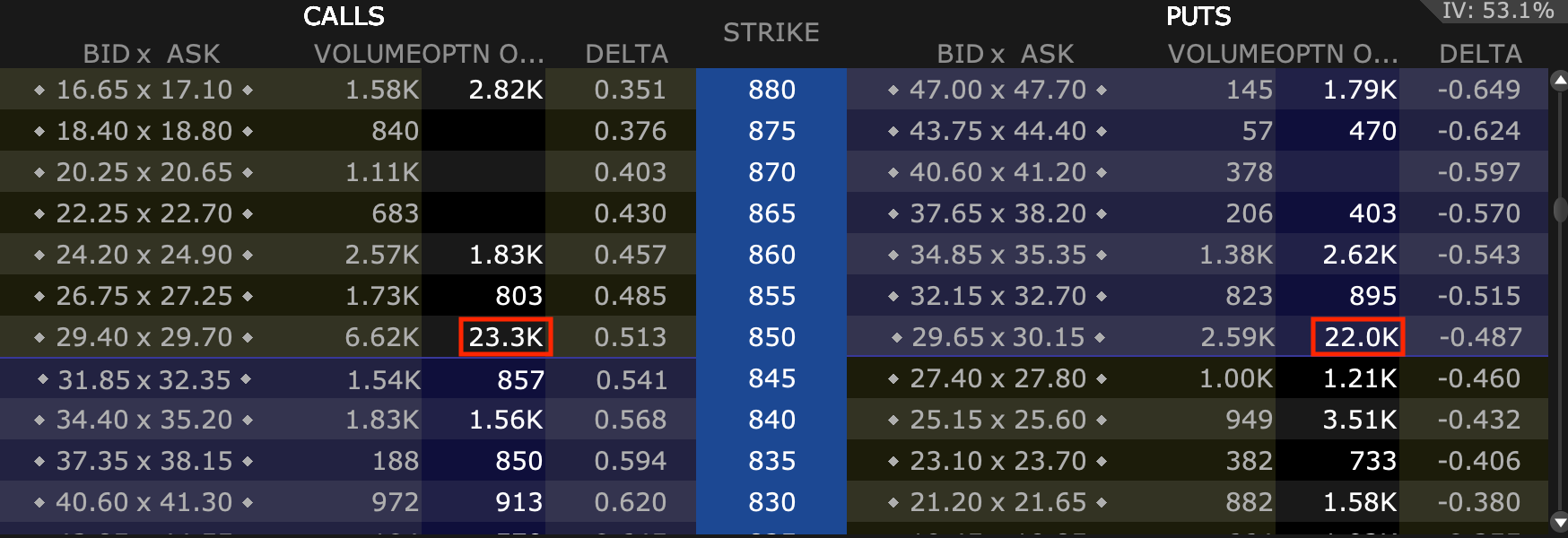
Stocks with high open interest in their options markets tend to see their options markets account for a material amount of the movement in the underlying stock.

Oftentimes, part of a market’s consolidation around certain whole-number prices (what some might call support and resistance) has to do with the “wall” of options at the whole-number strike prices.

This is due to the effect delta, gamma (a second-order Greek), and other potential influences have on hedging operations.

For example, you can see the high volume of options around the 850 strike price in this particular market (Tesla) relative to other less prominent whole numbers.

Potential delta-related support/resistance

Moneyness

Moneyness refers to the implied probability that an option will expire ITM.

Delta is similar but not exactly equal to moneyness. For example, an ATM call option typically has a delta of around 0.50, and a minus-0.50 delta for an ATM put option. This makes sense because there’s about a 50 percent probability of the option landing ITM.

ATM calls tend to have a somewhat higher delta than ATM puts for most risk assets because of the discount factor that implies that they’ll increase in value in the future.

Similarly, a trader might think there’s a 25 percent chance of an option landing ITM if its delta is 0.25.

Dual Delta

The actual probability of an option finishing ITM is called the dual delta.

Dual delta is the first derivative of an option price with respect to strike.

Put And Call Relationship

Given the same underlying, strike price, time to maturity, and no dividend yield, the sum of deltas for each option is one.

Namely, the sum of the delta of the call – a positive value – and the sum of the delta of the put – a negative value – will be one.

If the delta of a call is 0.58, the delta of a put can be observed – or calculated to be in the absence of this information – to be minus-0.42.

In the real world, there is generally some deviation.

Therefore, we can say that the following are true:

∆(call) – ∆(put) = 1

∆(call) = ∆(put) + 1

∆(put) = ∆(call) – 1