Adaptive Filtering Techniques in Finance

Adaptive filtering techniques in finance enable the creation and adjustment of predictive models in real-time.

Fundamentally, in trading contexts, how do changes in the value of input variables lead to certain trading decision(s))?

Adaptive filtering techniques help with these fundamental analysis tasks, which makes them valuable for various financial applications including algorithmic trading, risk management, and various forms of market analysis.

Adaptive filters adjust their parameters automatically to match the statistical properties of the input signal.

In finance, this could be asset prices, trading volumes, or economic indicators, among other variables.

This adaptability is important in finance, where market conditions and data patterns change in unique ways.

Key Takeaways – Adaptive Filtering Techniques

• Real-Time Adaptation
  • Adaptive filters adjust to changing data (e.g., market or economic conditions) in real-time.
  • Enables traders to maintain “optimal” trading strategies amidst volatility and factors that might cause discretionary traders to trade sub-optimally.
• Error Minimization
  • These techniques continuously correct prediction errors.
  • Improves the accuracy of forecasts and reduces potential losses.
• Noise Reduction
  • By filtering out market noise, adaptive techniques help traders identify genuine trends and signals.
• Applications
  • Market Trend Analysis – Identifying underlying trends in noisy financial time series data.
  • Risk Management – Estimating/filtering out noise in volatility measurements.
  • High-Frequency Trading – Cleaning high-frequency financial data to identify actionable trading signals against market noise.
  • Algorithmic Trading Strategy Development – Better signal detection by filtering out irrelevant market noise from trading signals.
  • Economic Data Analysis – Improving the clarity of economic indicators by filtering out noise (more accurate macroeconomic analyses).
  • Portfolio Optimization – Filtered asset return data for dynamic portfolio rebalancing, and better risk-adjusted returns.
  • Execution Cost Analysis – Analyzing and minimizing market impact and execution costs by distinguishing between genuine market movements and noise.
• Math & Coding Example
  • We cover some basic adapative filtering math, plus a coding example below.

Key Concepts

The key concepts adaptive filtering techniques include:

Adaptation Mechanism

The core of adaptive filtering is its ability to change filter parameters in response to an evolving input signal.

This mechanism ensures that the filter’s output remains optimal or near-optimal as the statistical characteristics of the input data change over time.

Online Learning

Adaptive filters are designed to learn and update their parameters in real-time or on a sequential basis, as opposed to batch processing.

This is essential in finance, where timely information is important for decision-making.

Error Correction

These filters typically use an error-correction mechanism where the difference between the actual output and the desired output is used to adjust the filter parameters.

This approach minimizes prediction errors and enhances model accuracy.

Signal Prediction

Adaptive filtering techniques are often used for predicting future values of financial time series.

This includes forecasting asset prices, interest rates, or economic indicators based on historical and other forms of data.

Noise Reduction

They’re effective in reducing noise from financial data.

This helps to identify underlying trends and patterns.

Adaptive filtering is useful in high-frequency trading, where price signals can be contaminated with market noise.

Types of Adaptive Filtering Techniques

Least Mean Squares (LMS)

This algorithm adjusts the filter coefficients to minimize the mean square error between the desired signal and the actual signal.

LMS is straightforward to implement and is widely used in financial engineering for its simplicity and efficiency.

Recursive Least Squares (RLS)

RLS offers faster convergence than LMS – at the cost of increased computational complexity.

It’s effective in environments where the statistical properties of the signal change rapidly.

It’s most suitable for adaptive risk management models and portfolio optimization.

Kalman Filter

This is a popular technique for estimating the state of a linear dynamic system from a series of incomplete and noisy measurements.

In finance, Kalman filters are used for estimating hidden states in financial markets.

A hidden state in financial markets could be the “intrinsic value of a stock,” which is not directly observable but influences its price movements and can be estimated through adaptive filtering techniques like the Kalman filter.

Namely, the theoretical value of a stock is the present value of future cash flows, though the actual market price is always changing due to the unique motivations, influences, and behaviors of market participants.

Adaptive Moving Averages

Most traders are familiar with the concept of moving averages.

These are used to smooth financial time series data while dynamically adjusting the smoothing parameter based on the volatility of the data.

This technique is useful for identifying trends.

Neural Networks

Adaptive neural networks can learn complex nonlinear relationships in financial data.

They adjust their weights and biases in response to new information.

This makes them suitable for various forecasting, trading, and risk management applications.

Particle Filters

These are advanced Monte Carlo algorithms used for estimating the posterior distribution of state-space models.

(State-space models are mathematical frameworks that describe a system’s dynamics in terms of inputs, outputs, and internal states, which allow for the analysis and prediction of time-related behaviors in systems such as financial markets.)

Particle filters are useful in finance for non-linear filtering problems, such as tracking the state of the economy or estimating the time-varying risk premia (e.g., the yield on BBB corporate bonds vs. the “yield” on stocks).

Gradient Descent

Used in LMS and other adaptive algorithms to find the filter weights that minimize the error criterion.

This technique iteratively adjusts the weights in the opposite direction of the gradient of the error surface with respect to the weights.

Related: Gradient Descent

Stochastic Gradient Descent (SGD)

A variant of gradient descent that updates the filter weights using a subset of the data (or even a single data point) at each iteration, which makes it suitable for online and real-time processing in financial applications.

Wiener Filter

A non-adaptive filtering approach that provides a theoretical foundation for adaptive filters.

It’s the optimal linear filter for minimizing the mean square error between the desired signal and the actual signal, given stationary signal and noise statistics.

Signal-to-Noise Ratio (SNR) Improvement

Adaptive filters try to improve the SNR by suppressing noise while retaining the signal of interest.

This concept is central to the effectiveness of adaptive filtering in enhancing signal quality.

Covariance Matrix Adaptation

Used in more advanced adaptive filtering techniques.

This approach adapts the filter based on the covariance of the input signals.

Allows for more sophisticated adaptation in complex signal environments.

Spectral Analysis

Involves analyzing the frequency components of signals.

Can be important for designing and tuning adaptive filters, especially in applications requiring the separation of signals from noise in specific frequency bands.

Eigenvalue and Eigenvector Analysis

Relevant in advanced adaptive filtering techniques, such as in the analysis of the convergence properties of the filter and in understanding the behavior of the filter in multidimensional signal spaces.

Applications of Adaptive Filtering Techniques

Here are some example applications where such adaptive filtering techniques could be valuable:

1. Trend Following and Market Anomaly Detection

Adaptive filters can be used to detect trends and anomalies in financial time series data, such as stock prices or indices.

By filtering out the noise, traders and algorithms can more accurately identify underlying trends or sudden market movements, which might indicate investment/trading opportunities or risks.

2. High-Frequency Trading (HFT)

In HFT, algorithms execute orders at extremely high speeds, often capitalizing on very small price differences.

Adaptive filters can help in cleaning noisy market data in real-time.

This allows HFT algorithms to make more informed decisions based on the underlying price movements rather than on transient noise.

3. Risk Management

Adaptive filtering can assist in estimating the volatility of financial instruments more accurately by filtering out the noise from the return series.

This can lead to better risk assessments and hedging strategies, as the filtered data can provide a clearer view of the underlying risk factors.

4. Portfolio Optimization

Portfolios can benefit from adaptive filtering by using it to extract and predict underlying asset return trends from noisy market data.

This information can then be used to dynamically adjust portfolio weights to optimize for risk-adjusted returns and adapt to changing markets in a more informed manner.

5. Economic Indicator Analysis

Economists and financial analysts can use adaptive filtering to clean economic indicator data.

This includes GDP growth rates or inflation figures, which are often subject to revisions and noise.

A clearer signal on the economic indicators can provide better insights into macroeconomic trends, which can influence trading/investment decisions and policymaking.

6. Signal Processing for Algorithmic Trading

Similar to its use in HFT, adaptive filtering can be employed in more traditional algorithmic trading strategies to process and clean historical data for backtesting, as well as to filter live market data for signal generation.

This can help in creating better trading models that are less prone to overfitting and better at capturing the true market dynamics.

7. Market Impact and Execution Analysis

Traders and institutions can use adaptive filtering to analyze liquidity, and the market impact of their trades, and optimize their execution strategies accordingly.

By filtering out market noise, they can better understand the actual impact of their trades on market prices.

This can lead to more efficient trade execution with minimized market impact.

Overall

In all these applications, the key advantage of using adaptive filtering techniques is their ability to dynamically adjust to changes in data and values of input variables.

This improves the signal-to-noise ratio in financial data analysis.

This, in turn, leads to more accurate predictions, optimizations, and assessments.

Math Behind Adaptive Filtering Techniques

Here’s an overview of some of the key mathematical concepts behind adaptive filtering techniques in finance:

Recursive Least Squares (RLS) Filter

• Used to estimate and update a model as new data becomes available
• Minimizes the sum of squared residuals between actual values and predicted values

Mathematical model:

θ̂n = θ̂n-1 + gn*en

Where:

• θ̂ = parameter estimate vector
• gn = Kalman gain vector
• en = error term

Kalman Filter

• Special case of RLS filter where the systems are assumed to have Gaussian noise
• Model includes state transition and observation equations

Here are the key equations:

State Update:

xn = Anxn-1 + Bnun + wn

• xn is the current state vector
• An is the state transition matrix – it captures the dynamics of the state from the prior to current time step
• xn-1 is the prior state vector
• Bn maps the control inputs un to the state
• wn is the process noise (assumed Gaussian)

So this updates the current state based on the previous state and the system dynamics.

Covariance Update:

Pn = AnPn-1ATn + Qn

• Pn is the covariance matrix of the current state
• AnPn-1ATn propagates the covariance from the previous to current time step
• Qn models the process noise

So this propagates forward the uncertainty in the state estimate.

Kalman Gain:

Kn = PnHTn(HnPnHTn + Rn)-1

• Kn optimally weights the measurements and current predicted state
• Hn maps current state to measurements
• Rn is the measurement noise

This calculates the optimal gain to apply to the measurement residual.

Output Estimate:

yn = Hnxn

• yn is the current output
• Hn converts current state into output measurements

So it uses the updated state estimate to produce an output prediction.

In short, these equations propagate forward the state and covariance estimates over time while incorporating the measurements to correct the predicted state – i.e., optimizes the balance between predictions and measurements.

Where:

• A, B, H = System matrices
• Q, R = Covariance matrices of process and measurement noise

Particle Filters

• Non-linear Bayesian tracking methodology
• Represent probability distributions as set of discrete samples (particles)
• Particles evolve and adapt to new data
• Weights are updated based on new observations
• Key computations involve statistical distances between particle parameters

Summary

Adaptive filters in finance leverage mathematical techniques like RLS, Kalman filtering, and particle filtering to dynamically update model states and parameters as new data arrives.

This allows strategies to flexibly adapt as input variables evolve.

Coding Example – Adaptive Filtering Techniques

Let’s create a Python example that demonstrates an adaptive filtering technique using the Least Mean Squares (LMS) algorithm.

The LMS algorithm will adjust its weights to minimize the error between the predicted value and the actual value on a set of cyclical data. (This will conceptually show how it can adapt to changing market conditions.)

import numpy as np
import matplotlib.pyplot as plt

# Settings
np.random.seed(55)
n_samples = 1000 # number of samples
n = 10 # number of filter weights
mu = 0.01 # step size (learning rate)

# Generate a sample signal (e.g., a sine wave)
t = np.linspace(0, 1, n_samples)
original_signal = np.sin(2 * np.pi * 5 * t)

# Add noise to the signal
noise = np.random.normal(0, 0.5, n_samples)
noisy_signal = original_signal + noise

# Initialize the LMS adaptive filter
weights = np.zeros(n)
output_signal = np.zeros(n_samples)
error_signal = np.zeros(n_samples)

# Adaptive filtering using LMS
for i in range(n, n_samples):
    # Input vector (sliding window of the noisy signal)
    input_vector = noisy_signal[i-n:i]

    # Filter output (dot product of input vector & weights)
    output_signal[i] = np.dot(input_vector, weights)

    # Error (difference between actual signal & filter output)
    error_signal[i] = original_signal[i] - output_signal[i]

    # Update the weights
    weights += 2 * mu * error_signal[i] * input_vector

# Plot results
plt.figure(figsize=(15, 5))
plt.plot(t, original_signal, label='Original Signal')
plt.plot(t, noisy_signal, label='Noisy Signal', alpha=0.5)
plt.plot(t, output_signal, label='Output Signal (Filtered)')
plt.legend()
plt.title('Adaptive Filtering using LMS Algorithm')
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.show()

Results

The algorithm updates its weights each day to minimize the prediction error, which demonstrates how adaptive filters can adjust to new data.

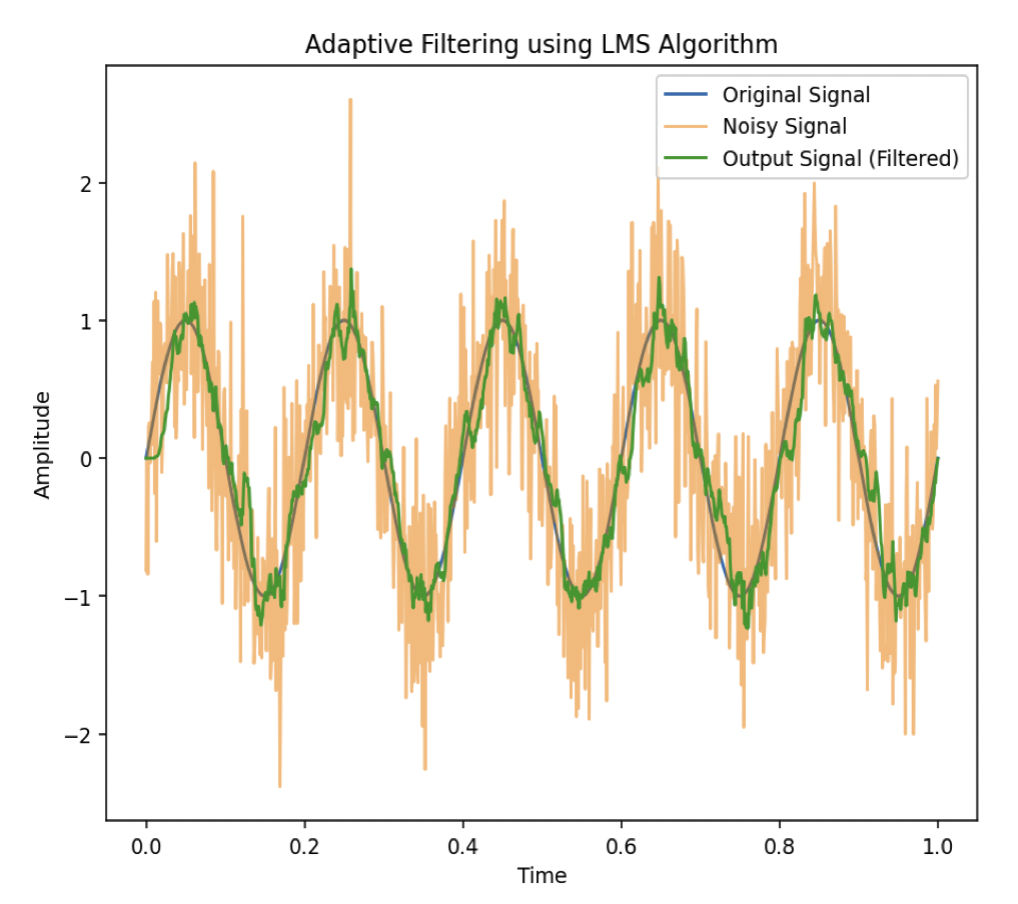
(This is a basic demonstration and in real-world applications, more complex features and adaptive algorithms may be used for better prediction accuracy.)

Conclusion

Adaptive filtering techniques are a more sophisticated set of tools for financial analysis and decision-making.

They’re valuable in managing the unknowns and unique dynamics of financial markets to provide a better framework for predictive modeling and risk assessment.

Related: Regime-Switching Models