Gradient-Based Methods in Quantitative Finance

Gradient-based methods are a category of optimization techniques used in quantitative finance.

They use the concept of a gradient, which is a vector indicating the direction of the steepest ascent of a function.

These methods are particularly effective in scenarios involving continuous and differentiable objective functions.

Key Takeaways – Gradient-Based Methods in Quantitative Finance

• Gradient Descent:
  • Gradient Descent is a fundamental optimization algorithm used in machine learning and quantitative finance.
  • It iteratively adjusts parameters to minimize a cost function.
  • It moves in the direction of the steepest descent as defined by the negative of the gradient.
• Stochastic Gradient Descent (SGD):
  • Stochastic Gradient Descent is a variant of gradient descent where updates to parameters are made using a subset of data (a mini-batch) rather than the entire dataset.
  • This approach can lead to faster convergence with large datasets.
    • But it may introduce more noise in the optimization path.
• Conjugate Gradient Method:
  • The Conjugate Gradient Method is an algorithm for the numerical solution of particular systems of linear equations, specifically those whose matrix is symmetric and positive-definite.
  • It is often used in optimization problems in finance as it can be more efficient than the standard Gradient Descent, especially for large systems.
• Newton-Raphson Method:
  • The Newton-Raphson Method is a root-finding algorithm that uses first and second derivatives to find successively better approximations to the roots (or zeroes) of a real-valued function.
  • In optimization, it is used for finding the maximum or minimum of a function and is known for its quadratic convergence.
  • It requires the calculation of second derivatives.

Gradient Descent

Gradient Descent is an iterative optimization algorithm used to find the local minimum of a function.

Gradient Descent is used in finance for optimizing financial models, such as in portfolio optimization or risk management.

It iteratively adjusts parameters to minimize a cost function. This enhances the accuracy and efficacy of predictions and decisions.

The method involves taking steps proportional to the negative of the gradient (or approximate gradient) of the function at the current point.

It’s widely used due to its simplicity and effectiveness in a variety of applications.

Application in Quantitative Finance

As mentioned, Gradient Descent is employed in tasks such as minimizing cost functions, calibrating models to market data, and optimizing investment strategies.

It’s particularly effective in scenarios where the objective function is convex and differentiable*, such as in mean-variance portfolio optimization and in the calibration of certain financial models.

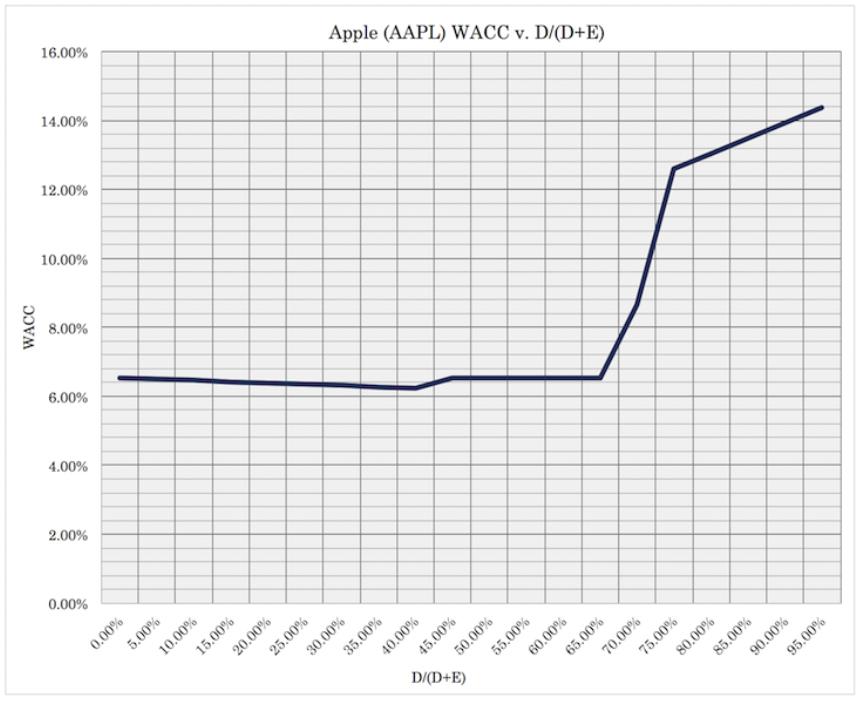
In our article on Apple stock, we also discussed how the company’s capital structure can be modeled via a curve.

This is essentially an optimization problem.

Taking the minimum point of this curve can be thought of as the “optimal capital structure” (i.e., the right mix of debt and equity) to maximize the company’s value.

__

* “Convex and differentiable” refers to a type of function that curves (convex) and can be smoothly differentiated at every point. This provides a clear direction for gradient descent to efficiently find the minimum value.

Stochastic Gradient Descent (SGD)

Stochastic Gradient Descent is a variation of the gradient descent algorithm that updates the model’s parameters using only a single or a few training examples at a time.

It is especially useful for large datasets because it reduces the computational burden.

It provides faster iterations in exchange for a higher variance in the parameter updates.

Application in Quantitative Finance

SGD finds its applications in quantitative finance in areas such as large-scale risk modeling and in the development of complex trading algorithms.

It is particularly advantageous for real-time financial modeling and high-frequency trading – where the ability to process vast amounts of data quickly is the #1 priority.

Conjugate Gradient Method

The Conjugate Gradient Method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is symmetric and positive-definite.

It is often used when the system is too large to be handled by direct methods (such as the Cholesky decomposition).

Application in Quantitative Finance

In finance, it’s often employed for optimizing large-scale portfolio problems

It is particularly valuable when dealing with large, sparse matrices, which are common in financial modeling.

Basically, it’s useful where you need to make decisions but don’t have a clear or easy way to see how everything fits together.

Newton’s Method

Newton’s Method, also known as the Newton-Raphson method, is a technique for finding successively better approximations to the roots (or zeroes) of a real-valued function.

The method uses the first and second derivatives of a function to rapidly converge to a solution.

Application in Quantitative Finance

Newton’s Method is used in quantitative finance for optimizing non-linear models, particularly in the calibration of complex financial models to market data.

It’s effective in scenarios where higher-order derivative information is available and can significantly accelerate the convergence to an optimal solution compared to basic gradient descent.

Conclusion

Gradient-based methods, including Gradient Descent, Stochastic Gradient Descent, the Conjugate Gradient Method, and Newton’s Method, are used in quantitative finance.

They are used extensively for optimizing trading/investment strategies, calibrating models, and managing risks.

Especially in contexts where objective functions are continuous, differentiable, and, ideally, convex (so optimum points can be found).

Their efficiency in handling large datasets and complex mathematical models makes them useful tools in financial analytics and modeling.