Ultima (Option Greek)

Ultima is a third-order derivative of the option value with respect to volatility.

In other words, it’s an advanced option Greek that measures the sensitivity of an option’s Vomma (second-order sensitivity) to changes in volatility.

This makes it one of the more complex Greeks used in options trading and risk management.

Key Takeaways – Ultima (Option Greek)

• Ultima is the third-order sensitivity of the option’s value to volatility.
• Ultima measures the rate of change in Vomma as volatility shifts, providing better insight into options’ behavior during extreme market moves.
  • Traders can use this to optimize positions in volatile environments or when understanding the nuances effects of volatility is important.
• Positive Ultima indicates accelerating Vomma as volatility increases, often seen in out-of-the-money options.
  • This property can be exploited for volatility-of-volatility trading strategies.
• Ultima is valuable for complex options strategies and risk management, where knowing how lower-order Greeks change in response to volatility is important.

Definition

Ultima is mathematically expressed as:

Ultima = ∂Vomma / ∂σ = ∂³V / ∂σ³

Where:

• V is the option value
• σ (sigma) represents volatility

Ultima is also sometimes referred to as DvommaDvol, highlighting its relationship to Vomma and volatility.

The Role of Ultima in Options Trading

Relationship to Other Greeks

To understand Ultima’s significance, it’s important to consider its relationship to other option Greeks:

1. Delta – An option’s first-order sensitivity to price changes
2. Gamma – Second-order sensitivity to price changes
3. Vega – First-order sensitivity to volatility changes
4. Vomma – Second-order sensitivity to volatility changes
5. Ultima – Third-order sensitivity to volatility changes

This progression shows how Ultima represents a higher-level analysis of an option’s behavior in response to volatility changes.

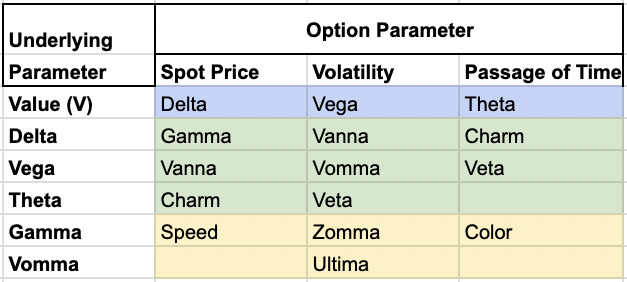
Greek Hierarchy

Let’s look at Ultima’s place in the hierarchy of option Greeks:

1. First-order Greeks – Delta, Vega, Theta, Rho*
2. Second-order Greeks – Gamma, Vanna, Charm, Vomma
3. Third-order Greeks – Speed, Zomma, Color, Ultima

As mentioned, Ultima belongs to the third-order Greeks, meaning it measures the rate of change of second-order Greeks.

*Rho is less common and typically not listed on charts of the Greek sensitivities.

Practical Applications

Ultima is primarily used by sophisticated options traders, market makers, and risk managers who need to understand and manage the nuanced effects of volatility on their portfolios.

Some key applications include:

1. Risk management in volatile markets
2. Fine-tuning of complex options strategies
3. Volatility trading and arbitrage
4. Pricing of exotic options

Calculating Ultima

Mathematical Approach

Calculating Ultima involves complex mathematical models.

It typically requires numerical methods due to the lack of closed-form solutions for most option pricing models.

The Black-Scholes model, while limited in its assumptions, can provide a basis for understanding Ultima’s calculation.

Sophisticated market makers and quantitative hedge funds will use their own models.

As a result, Greek calculations aren’t exactly the same.

Factors Affecting Ultima

Several factors influence the value of Ultima:

1. Time to expiration
2. Strike price
3. Underlying asset price
4. Interest rates
5. Dividend yield (for stock options)
6. Current volatility level

Interpreting Ultima Values

Positive vs. Negative Ultima

• Positive Ultima – Indicates that Vomma increases as volatility rises
• Negative Ultima – Suggests that Vomma decreases as volatility increases

Magnitude of Ultima

The absolute value of Ultima provides insight into the sensitivity of Vomma to volatility changes.

Larger absolute values indicate greater sensitivity.

What this means depends on the strategy, as far as taking positions, hedging, etc.

Ultima in Different Option Types

Call Options

Call options generally have:

• positive Ultima for out-of-the-money strikes
• negative Ultima for in-the-money strikes.

Put Options

Put options typically display the opposite behavior, with:

• negative Ultima for out-of-the-money strikes and
• positive Ultima for in-the-money strikes

Trading Strategies Using Ultima

Volatility of Volatility Trading

Traders focusing on the volatility of volatility can use Ultima to fine-tune their positions and manage risk.

Complex Option Spreads

Advanced spread strategies, such as butterfly spreads or condors (or analogous trade structures), can be optimized by considering Ultima alongside other Greeks.

Ultimate Trade Example: Exploiting Volatility of Volatility in a Tech Stock

Here we’ll outline a step-by-step example of an Ultima trade that an options trader or market maker might execute.

This example will demonstrate how Ultima can be used in practice and explain the purpose behind such a trade.

Let’s consider a scenario involving a large tech company (we’ll call it TechCorp) that’s about to release its quarterly earnings report.

The market is expecting significant volatility around this event.

Step 1: Market Analysis

The trader observes that implied volatility for TechCorp options is already high due to the upcoming earnings announcement.

However, they believe that the market is underestimating the potential for even larger volatility swings.

Step 2: Ultima Calculation

The trader calculates the Ultima for various strike prices and expiration dates of TechCorp options.

They notice that out-of-the-money (OTM) call options with expirations just after the earnings date have particularly high positive Ultima values.

Step 3: Strategy Selection

Based on this analysis, the trader decides to implement a long Vomma strategy that will benefit from an increase in the volatility of volatility.

They choose to focus on OTM call options due to their high positive Ultima.

Step 4: Position Entry

The trader buys a strangle position:

• Buy 10 contracts of TechCorp 110 Call options (current stock price: $100)
• Buy 10 contracts of TechCorp 90 Put options Both options expire two weeks after the earnings announcement.

Step 5: Hedging

To minimize directional risk, the trader Delta-hedges the position by shorting or longing the appropriate amount of TechCorp stock based on the overall Delta of the options position.

Step 6: Monitoring

The trader closely monitors the position, paying particular attention to changes in implied volatility and the options’ Vega and Vomma.

Note that this is impossible to calculate by hand and would be done with specialized software or algorithmic models.

Even trades themselves are typically executed algorithmically, given it’s faster, cheaper, more accurate, less biased, and less emotional than a human.

Step 7: Volatility Spike

As anticipated, implied volatility increases sharply in the days leading up to the earnings announcement.

The positive Ultima of the OTM call options causes their Vomma to increase significantly, leading to accelerated gains in the option prices.

Step 8: Position Adjustment

The trader may need to readjust their Delta hedge as the stock price and implied volatility change.

Step 9: Exit

After the earnings announcement, when implied volatility begins to decrease, the trader closes out the position, having profited from the increase in the volatility of volatility.

Purpose of the Trade

The primary purpose of this trade is to profit from an expected increase in the volatility of volatility, rather than from a directional move in the underlying stock price.

Here’s why this trade leverages Ultima:

Volatility Exposure

The long strangle position provides exposure to increases in implied volatility (positive Vega).

Vomma Acceleration

The high positive Ultima of the OTM call options means that as volatility increases, the Vomma of these options increases as well.

This leads to an accelerating increase in the options’ prices as volatility rises.

Risk Management

By choosing options with high Ultima, the trader maximizes their exposure to changes in the volatility of volatility while minimizing the capital required for the trade.

Market Making

For a market maker, understanding and trading on Ultima can help in more accurate pricing of options, especially during periods of heightened volatility.

Hedging

This strategy could also be used as a hedge for a portfolio that is vulnerable to large, unpredictable swings in volatility.

Overall

This trade example demonstrates how advanced option traders can use higher-order Greeks like Ultima to fine-tune their strategies and potentially profit from complex market dynamics that may be overlooked by less sophisticated market participants.

Nonetheless, such strategies are complex and require a deep understanding of options mechanics and market behavior.

They are very difficult to successfully pull off for a discretionary trader.

Limitations & Considerations

Model Dependency

Ultima’s accuracy is highly dependent on the option pricing model used.

Different models may produce varying Ultima values, especially for exotic options.

Market Liquidity

In illiquid markets, the theoretical Ultima may not accurately reflect real-world trading conditions.

Practical Implementation Challenges

Due to its complexity, implementing Ultima in real-time trading systems can be computationally intensive and will more or less require sophisticated software.

Ultima in Risk Management

Portfolio-Level Analysis

Risk managers use Ultima to assess the overall sensitivity of option portfolios to extreme changes in volatility.

Stress Testing

Ultima can be incorporated into stress testing scenarios to model the behavior of option portfolios under severe market conditions.

Future Developments & Research

This is our last article in the series of option Greeks that we’ll be covering.

While we could also cover higher-order Greek beyond this, like how Ultima changes in response to volatility and so on, we’re at the point of diminishing returns, which is why these hypothetical 4th- and nth-order Greeks aren’t traditionally talked about.

Some basics on how things are trending:

Machine Learning Applications

More and more financial analysis is going toward machine learning where computers are tasked with figuring things out with various levels of supervision.

It explores the use of machine learning algorithms to predict and analyze Greeks and other sensitivities and parameters more efficiently.

Integration with Other Risk Metrics

Ultima is one sensitivity. You can have a whole dashboard of risk metrics and all weighted appropriately based on the strategy.

Conclusion

Ultima represents a multi-order sensitivity in options risk analysis, measuring more nuanced volatility of volatility situations – i.e., studying the behavior of options under changing volatility conditions.

Its complexity and relevance under select circumstances limits its use to advanced traders and risk managers, but understanding Ultima can offer advantages in options trading and risk management – or at least prevent disadvantage.

But overall, Ultima is just one sensitivity in options risk management and should be used in conjunction with other analyses and sound financial principles.