Vega (Option Greek)

Vega is one of the “Greeks” used in options trading and risk management.

It measures the sensitivity of an option’s price to changes in the underlying asset’s implied volatility.

Vega is an important concept for options traders and investors to understand, as it provides insights into how volatility affects option prices.

Key Takeaways – Vega

• Vega measures an option’s price sensitivity to volatility changes.
• A 1% increase in implied volatility raises an option’s price by its Vega value, helping traders quantify volatility risk.
• At-the-money options with more time to expiration have higher Vega.
  • This makes them more sensitive to volatility shifts, which is important for strategies like straddles or strangles.
• Being long options means being long Vega.
  • Traders long Vega profit from volatility increases but lose on decreases, important for both directional and volatility-focused strategies.

Definition and Calculation

What is Vega?

Vega represents the rate of change in an option’s price for every 1% change in implied volatility.

It’s expressed as a monetary amount and is typically quoted per 1% change in volatility.

Calculation

The formula for Vega involves partial derivatives.

In practice, options pricing models like the Black-Scholes model are used to calculate Vega.

The general formula is:

Vega = ∂V / ∂σ

Where:

• V is the option’s price
• σ (sigma) is the implied volatility

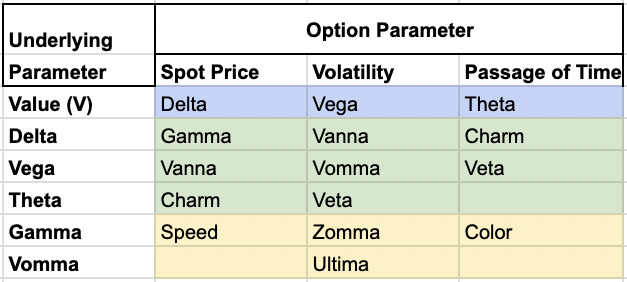
Characteristics of Vega

Positive Value

Vega is always positive for both call and put options.

This means that an increase in implied volatility will generally increase the option’s price, while a decrease will lower it.

Time Decay

Vega tends to be highest for at-the-money options and decreases as the option moves further in-the-money or out-of-the-money.

It also typically decreases as the option approaches expiration.

Relationship with Option Price

Options with higher prices generally have higher Vega values, as they have more extrinsic value that can be affected by changes in implied volatility.

Importance in Options Trading

Risk Management

Traders use Vega to assess and manage their exposure to volatility risk.

By understanding an option’s Vega, traders can anticipate how changes in implied volatility might affect their positions.

Volatility Trading Strategies

Some traders specifically target Vega in their strategies, trying to profit from changes in implied volatility rather than directional movements in the underlying asset.

Portfolio Hedging

Vega can be used to hedge a portfolio against volatility risk.

By balancing positive and negative Vega exposures, traders can create portfolios that are less sensitive to volatility changes.

Long Vega

Options are partly priced off implied volatility.

If you’re long options, you’re long vega – by and large.

There are some small nuances to this:

For deep in-the-money options, the Vega is relatively low compared to at-the-money options.

While technically still positive, the Vega’s impact is minimal, which makes the option’s sensitivity to volatility changes less significant.

Options with very short time to expiration have low Vega because there’s less time for volatility to affect the option’s price.

Even if you’re long these options, the Vega might be so small that changes in volatility have negligible effects.

Short Vega

Conversely, if you’re short options, you’re short vega.

Factors Affecting Vega

Time to Expiration

Options with more time until expiration generally have higher Vega values, as there’s more uncertainty about future price movements.

Strike Price

At-the-money options typically have the highest Vega, while deep in-the-money or out-of-the-money options have lower Vega values.

Underlying Asset Volatility

The current level of implied volatility can affect Vega.

Options on assets with high implied volatility may have different Vega characteristics compared to those with low implied volatility.

Practical Applications

Option Pricing

Understanding Vega helps traders more accurately price options, especially when markets are changing rapidly.

Spread Strategies

Many spread strategies, such as calendar spreads or butterfly spreads, are designed to take advantage of or reduce Vega exposure.

Volatility Surface Analysis

Advanced traders use Vega in conjunction with other Greeks to analyze and trade the entire volatility surface of an options chain.

Vega Hedging

Vega hedging involves adjusting a portfolio to neutralize the sensitivity of an option’s price to changes in volatility.

This is typically achieved by adding or removing options with opposing Vega exposures.

When the overall portfolio Vega is zero or close to zero, this helps minimize the impact of volatility fluctuations.

Many, but not all, brokers provide Vega readings within a portfolio’s dashboard.

Limitations and Considerations

Model Dependence

Vega calculations are based on theoretical models, which may not accurately reflect real-world market conditions.

Non-linear Behavior

In practice, the relationship between volatility changes and option prices is not always linear, especially for large moves in volatility.

Interaction with Other Greeks

Vega doesn’t exist in isolation.

Its effects on option prices can be influenced by changes in other factors, such as the underlying asset price (Delta) or time decay (Theta).

Conclusion

Understanding Vega is essential for anyone involved in options trading or risk management.

It show how volatility affects option prices and helps traders make more informed decisions about their positions and strategies.

Related: Aega, Rega, Sega