Zomma (Option Greek)

Zomma, also known as DGammaDVol, is a third-order Greek letter used in options trading and risk management. 

It measures the rate of change in an option’s Gamma with respect to changes in implied volatility. 

Zomma is part of the family of Greek letters that help traders, market makers, and risk managers understand and quantify the various sensitivities and parameters affecting option prices and risk exposures.

Key Takeaways – Zomma (Option Greek)

• Zomma measures how an option’s gamma changes with volatility, helping traders anticipate risk exposure shifts during market turbulence.
• Positive Zomma indicates increasing gamma as volatility rises, potentially amplifying profits (or losses) from gamma trading strategies.
• At-the-money options near expiration typically have the highest Zomma.
• We provide an example Zomma trade below.

Understanding Zomma in the Context of Option Greeks

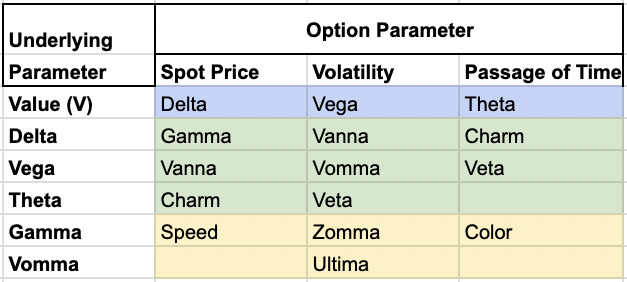
The Greek Letter Hierarchy

To fully grasp the concept of Zomma, it’s essential to understand its place in the hierarchy of option Greeks:

1. First-order Greeks – Delta, Vega, Theta, Rho*
2. Second-order Greeks – Gamma, Vanna, Charm, Vomma
3. Third-order Greeks – Speed, Zomma, Color, Ultima

Zomma belongs to the third-order Greeks, which measure the rate of change of second-order Greeks.

*Rho is often excluded on Greeks charts like the one below because it’s not as commonly used/considered.

Relationship to Gamma and Vega

Zomma is closely related to two important second-order Greeks:

1. Gamma – Measures the rate of change in an option’s delta with respect to the underlying asset’s price.
2. Vega – Measures the rate of change in an option’s price with respect to changes in implied volatility.

Zomma essentially combines aspects of both Gamma and Vega.

It lets options traders and market makers understand how Gamma changes as volatility fluctuates.

It’s used for Gamma-hedged portfolio to better understand how the hedge would work as volatility changes.

Mathematical Definition of Zomma

Formula

The mathematical formula for Zomma is:

Zomma = ∂³C / (∂S² ∂σ)

Where:

• C is the option price
• S is the underlying asset price
• σ (sigma) is the implied volatility

This formula represents the third partial derivative of the option price with respect to the underlying asset price (twice) and implied volatility (once).

Interpretation

A positive Zomma indicates that an option’s Gamma increases as volatility rises, while a negative Zomma suggests that Gamma decreases as volatility increases.

Practical Applications of Zomma

The most popular use of Zomma is understanding the risk profile of a Gamma-hedge portfolio under volatility fluctuations.

Risk Management

Zomma helps options traders, market makers, and risk managers in several ways:

1. Volatility exposure – It shows how changes in volatility affect an option’s Gamma, used for managing overall portfolio risk.
2. Hedging strategies – Traders can use Zomma to adjust their hedging strategies, particularly when dealing with large changes in volatility.
3. Stress testing – Zomma can be incorporated into stress tests to understand how a portfolio might behave under extreme market conditions.

Trading Strategies

Sophisticated options traders and market makers may use Zomma in developing and implementing advanced trading strategies:

1. Volatility trading – Zomma can help identify opportunities in volatility-based trades, particularly when combined with other Greeks.
2. Option spreads – When constructing complex option spreads, understanding Zomma can help in fine-tuning positions for specific market views.
3. Dynamic delta hedging – Traders engaged in dynamic hedging can use Zomma to anticipate how their hedging needs might change as markets change.

Factors Affecting Zomma

Several factors influence the value and behavior of Zomma:

Time to Expiration

As an option approaches expiration, its Zomma typically becomes more pronounced, especially for at-the-money options.

This reflects the increased sensitivity of Gamma to volatility changes as time decay accelerates.

Moneyness

The moneyness of an option (how far in-the-money or out-of-the-money it is) affects its Zomma.

At-the-money options generally have the highest absolute Zomma values, while deep in-the-money or out-of-the-money options have lower Zomma values.

Underlying Asset Characteristics

The nature of the underlying asset, including its historical volatility and market behavior, can impact Zomma values and their practical significance in trading and risk management.

Example Zomma Trade: Volatility Regime Change Anticipation

Scenario

An options trader believes that the market is about to transition from a low volatility environment to a high volatility environment. 

They want to position themselves to benefit from this anticipated change while managing their risk exposure.

Step 1: Initial Position Analysis

The trader starts with a Delta-neutral straddle position on a stock currently trading at $100:

• Long 1 ATM Call (Strike $100)
• Long 1 ATM Put (Strike $100)

This position is Gamma positive but vega positive as well.

This means it will benefit from increases in both stock price movement and implied volatility.

Step 2: Zomma Analysis

The trader calculates the Zomma of their position and finds it to be positive. 

This indicates that as volatility increases, the Gamma of their position will increase as well.

Step 3: Position Adjustment

To take advantage of the anticipated volatility increase and the positive Zomma, the trader decides to add to their position:

• Buy 2 OTM Call (Strike $105)
• Buy 2 OTM Put (Strike $95)

These OTM options have higher Zomma values than the ATM options, which will amplify the effect of the expected volatility increase on the position’s Gamma.

Step 4: Risk Management

To manage the increased risk from the additional options, the trader also:

• Sells 1 far OTM Call (Strike $110)
• Sells 1 far OTM Put (Strike $90)

This helps to partially offset the cost of the new options and provides some protection against extreme moves.

Step 5: Continuous Monitoring and Adjustment

The trader closely monitors the position, ready to make adjustments:

• If volatility increases as anticipated, they may begin to Delta hedge more actively due to the increased Gamma.
• If the stock price moves significantly, they may need to adjust the position to maintain delta neutrality.

Purpose of the Trade

1. Volatility Exposure – The primary goal is to benefit from an anticipated increase in market volatility. The positive Zomma position means that as volatility rises, the position’s gamma will increase, potentially leading to larger profits from stock price movements.
2. Gamma Scalping Opportunity – The increasing gamma (due to Zomma) as volatility rises creates more opportunities for profitable delta hedging (gamma scalping).
3. Risk Management – By using a combination of long and short options, the trader tries to structure a position that benefits from their market view while limiting potential losses.
4. Complexity Management – The trade allows the trader to take a nuanced position on market dynamics, going beyond simple directional or volatility bets.
5. Flexibility – The structure of the trade provides flexibility to adjust as market conditions change. This allows the trader to fine-tune their exposure.

Summary

This trade shows how advanced options traders can use higher-order Greeks like Zomma to construct positions that capture complex market views. 

Note that such trades require sophisticated understanding of options dynamics, continuous monitoring, and active management. 

Algorithms are practically always doing the work, as trades using Greeks are rarely done in a discretionary way.

Zomma is also a well-known variable (and has been since the 1990s) and is often integrated into analysis to avoid disadvantage rather than procuring an advantage.

The specific options chosen, their quantities, and strikes would be carefully calculated based on the trader’s precise market outlook, risk tolerance, the specific characteristics of the underlying asset, as well as the other components and structure of the portfolio.

Challenges & Limitations of Using Zomma

It’s important to consider Zomma’s limitations:

Complexity

As a third-order Greek, Zomma can be challenging to interpret and apply, especially for less experienced traders. 

Its effects may be subtle and easily overshadowed by more prominent risk factors.

It’s a much more nuanced concept.

Model Dependency

Like other Greeks, Zomma is model-dependent. 

Its values and implications can vary based on the option pricing model used (e.g., Black-Scholes vs. different more advanced models).

Market Liquidity

In less liquid markets or for exotic options, the practical application of Zomma may be limited due to wider bid-ask spreads and potential difficulties in executing trades based on its insights.

Conclusion

Zomma represents an advanced concept in options theory and risk management.

It may not be as widely used as first-order Greeks like Delta or even second-order Greeks like Gamma, but it’s still a sensitivity of interest for sophisticated traders, market makers, and risk managers.