Speed (Option Greek)

Speed is one of the lesser-known option Greeks.

Speed quantifies how quickly an option’s Gamma changes as the price of the underlying asset moves.

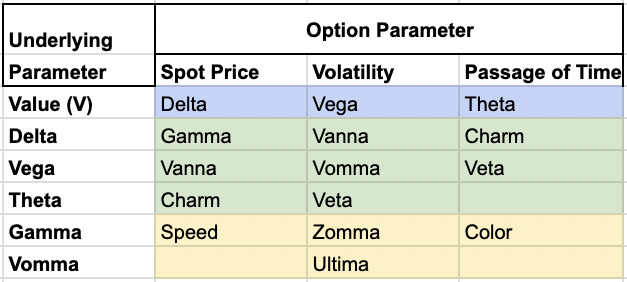
It’s the second derivative of the option’s Delta with respect to the underlying asset’s price.

It’s often referred to as the “Gamma of Gamma” or DgammaDspot (i.e., measured how Gamma changes with the spot price).

Key Takeaways – Speed (Option Greek)

• Speed measures the rate of change in an option’s gamma, alerting traders to potentially rapid shifts in delta.
  • This is used for maintaining delta-neutral positions most commonly in volatile markets.
• At-the-money options typically have the highest Speed, making them more sensitive to large price swings.
  • Traders should exercise caution when holding significant ATM positions.
• This behavior of Speed reflects the convexity and non-linear nature of options pricing.
• Positive Speed in calls (negative in puts) indicates increasing gamma as prices rise, potentially amplifying profits or losses.
  • This can inform decisions on position sizing and risk management.
• We give an example of a Speed trade below.

Understanding Speed in the Context of Option Greeks

Relationship to Delta and Gamma

To understand Speed, it’s good to first grasp the concepts of Delta and Gamma:

• Delta measures the rate of change in an option’s price with respect to changes in the underlying asset’s price.
• Gamma measures the rate of change in Delta with respect to changes in the underlying asset’s price.

Speed, then, can be thought of as the “Gamma of Gamma” or the second derivative of Delta.

It measures how Gamma changes as the underlying asset’s price changes.

Mathematical Expression

Speed is expressed mathematically as:

Speed = ∂³C / ∂S³

Where:

• C is the option price (sometimes referred to as V)
• S is the price of the underlying asset

This formula represents the third partial derivative of the option price with respect to the underlying asset price.

Importance of Speed in Options Trading

Risk Management

Speed is useful for traders and risk managers dealing with large option positions or complex option strategies.

It shows how quickly Delta and Gamma can change, which is important for maintaining Delta-neutral or Gamma-neutral positions.

Volatility and Price Movements

Speed becomes especially relevant during periods of high volatility or when the underlying asset experiences large price movements.

In these situations, understanding how quickly Delta and Gamma can change helps traders anticipate and manage potential risks more effectively.

Characteristics of Speed

Speed for Long Call Options

Out-of-the-Money (OTM)

For long call options that are OTM, the delta is relatively small and increases as the underlying price approaches the strike price.

Thus, the change in delta (which Speed measures) is positive.

In-the-Money (ITM)

For long call options that are ITM, the delta is close to 1 and increases at a decreasing rate as the underlying price rises further above the strike price.

Therefore, the Speed tends to be negative.

Speed for Long Put Options

Out-of-the-Money (OTM)

For long put options that are OTM, the delta is relatively small (in absolute value) and decreases as the underlying price approaches the strike price from below.

Thus, the change in delta is negative, making Speed negative.

In-the-Money (ITM)

For long put options that are ITM, the delta is close to -1 and becomes less negative (increases in absolute value) as the underlying price falls further below the strike price.

Accordingly, the Speed tends to be positive.

Magnitude of Speed

The magnitude of Speed tends to be largest for at-the-money (ATM) options and decreases as options move further ITM or OTM.

This reflects the fact that ATM options are most sensitive to changes in the underlying asset’s price.

Factors Affecting Speed

Several factors influence the value of Speed:

Time to Expiration

As an option approaches expiration, Speed generally increases in magnitude.

This is because time decay accelerates, causing more rapid changes in Delta and Gamma.

Volatility

Higher implied volatility typically leads to larger Speed values, as it increases the likelihood of significant price movements in the underlying asset.

Interest Rates

While less impactful than other factors, changes in interest rates can affect Speed, particularly for longer-dated options.

Applications of Speed in Trading Strategies

Dynamic Hedging

Traders use Speed to anticipate how quickly they may need to adjust their hedges.

This is important for maintaining delta-neutral positions when volatility is high.

Options Pricing Models

Advanced options pricing models might incorporate Speed to provide more accurate valuations, especially for exotic options or complex derivatives.

Risk Assessment

Portfolio managers use Speed to understand the potential for rapid changes in their portfolio’s risk profile.

Speed Hedge Trade Example: Protecting a Large Delta-Hedged Position

Purpose

The purpose of this hedge is to protect a large Delta-hedged options position against rapid changes in Gamma during high volatility periods.

Note that all of this will be done with algorithms that run these calculations.

Initial Position

Assume you have a large long position in at-the-money call options on Stock XYZ.

Say it’s currently trading at $100.

Step 1: Delta Hedge

• Calculate the position’s Delta and hedge it by shorting the appropriate amount of the underlying stock.

Step 2: Assess Speed Risk

• Calculate the position’s Speed.
• Let’s say it’s positive, indicating Gamma will increase rapidly if the stock price rises.

Step 3: Implement Speed Hedge

• To hedge against this Speed risk, enter a position with negative Speed.
• This could be achieved by selling out-of-the-money call options with a strike price of $110.

Step 4: Calibrate Hedge Size

• Determine the appropriate number of OTM calls to sell based on their speed and your desired hedge ratio.

Step 5: Monitor and Adjust

• Monitor the stock price, volatility, and time decay.
• As these factors change, recalculate Speed and adjust your hedge accordingly.

Outcome

If the stock price rises rapidly:

• Your original ATM calls gain value.
• Your short stock position loses money.
• Your short OTM calls provide a buffer against the rapid increase in Gamma of your long position.

This hedge helps stabilize your portfolio’s Gamma during large price movements, reducing the frequency and cost of rebalancing your Delta hedge.

It’s useful in high-volatility environments or when holding large positions where small changes can have significant impacts.

Limitations & Considerations

Complexity

Speed is a higher-order Greek, which makes it more complex to calculate and interpret.

Many traders focus primarily on Delta and Gamma, considering Speed only for large positions or sophisticated strategies.

Model Dependency

Like other Greeks, Speed values depend on the options pricing model used.

Different models may produce slightly different Speed values, especially for more complex options.

Market Liquidity

In illiquid markets, the theoretical Speed values may not accurately reflect real-world trading, as large trades can impact asset prices.

Conclusion

Speed, while not as commonly used as Delta or Gamma, provides additional insights into the behavior of option prices and risk profiles.

By measuring the rate of change in Gamma, it offers a deeper understanding of how an option’s sensitivity to price changes can evolve over time and under different market conditions (e.g., volatility/vega movements).

For advanced options traders and risk managers, incorporating Speed into their analysis can lead to more nuanced strategies and improved risk management.

It should be used in conjunction with other Greeks and financial metrics to form a thorough view of an option’s behavior and potential risks.

As trading strategies become increasingly sophisticated, understanding and using higher-order Greeks like Speed may become more important for maintaining a competitive edge – or at least avoid being disadvantaged – in options trading.