Vomma (Option Greek)

Vomma, also known as Volga or Vega Convexity, is an advanced concept in options trading and risk management.
It is one of the higher-order Greeks used to measure and manage the sensitivity of option positions.
Vomma shows how the Vega of an option changes as the underlying asset’s volatility fluctuates.
With positive Vomma, a position becomes long Vega as implied volatility increases and short Vega as Vomma falls.
Key Takeaways – Vomma
- Vomma measures how an option’s Vega changes with volatility shifts.
- Traders can create Vega-neutral, long-Vomma positions using option ratios.
- Provides opportunities to profit from volatility fluctuations while minimizing directional risk.
Definition and Basic Concept
What is Vomma?
Vomma is defined as the second derivative of the option price with respect to volatility.
In simpler terms, it measures the rate of change in an option’s Vega as the implied volatility of the underlying asset changes.
Mathematically, Vomma is expressed as:
Vomma = ∂²C / ∂σ²
Where C is the option price and σ (sigma) is the implied volatility.
Positive Vomma
Positive Vomma indicates that a position’s Vega sensitivity increases with rising implied volatility and decreases as volatility falls.
This characteristic allows for scalping opportunities similar to long gamma positions.
Vega Neutral, Long Vomma
Traders can create Vega-neutral, long-Vomma positions by using specific ratios of options at different strike prices.
Buying options with high Vomma and selling others to offset Vega (while keeping the positive Vomma) achieves this balance.
Long OTM Options = + Vomma
Long options that are out-of-the-money typically exhibit positive Vomma.
The Vomma initially grows as the strike moves further from the current price, but eventually diminishes as Vega decreases.
Mathematically, Vomma is positive when the Black-Scholes model‘s d1 and d2 terms have the same sign, which occurs when d1 < 0 or d2 > 0.
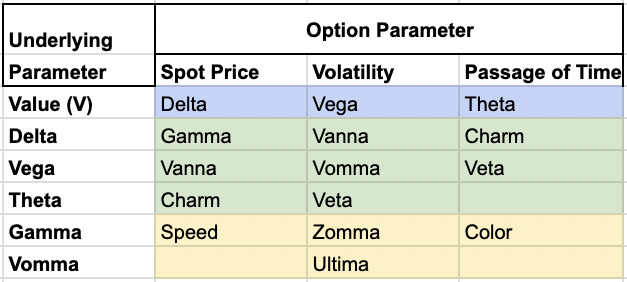
Relationship to Other Greeks
Vomma is closely related to other option Greeks, particularly Vega.
While Vega measures the first-order sensitivity of an option’s price to changes in implied volatility, Vomma takes this a step further by measuring the second-order sensitivity.
This relationship makes Vomma a valuable tool for traders and risk managers who need to understand and manage the non-linear behavior of options.
Importance in Options Trading
Understanding Vomma helps traders manage complex option positions and exploit volatility changes more effectively – especially in strategies involving multiple strikes or large volatility movements.
Risk Management
Vomma can be used in risk management for option portfolios.
It helps traders and risk managers anticipate and prepare for potential large moves in implied volatility, which can have significant impacts on option prices and overall portfolio values.
Volatility Trading Strategies
Traders who specialize in volatility-based strategies find Vomma most useful.
It helps traders understand how the effectiveness of their Vega-based trades might change as implied volatility evolves.
Pricing and Valuation
Understanding Vomma can lead to more accurate option pricing models and valuations.
Characteristics of Vomma
Positive vs. Negative Vomma
Vomma can be either positive or negative, depending on the option’s characteristics:
- Positive Vomma – Typically associated with out-of-the-money options. It indicates that the option’s Vega increases as volatility rises.
- Negative Vomma – More common in in-the-money options. It suggests that the option’s Vega decreases as volatility increases.
Factors Affecting Vomma
Several factors influence the magnitude and sign of Vomma:
- Moneyness – The degree to which an option is in-the-money or out-of-the-money affects its Vomma.
- Time to expiration – Vomma tends to be more pronounced for options with longer times until expiration.
- Implied volatility levels – The current level of implied volatility can impact the behavior of Vomma.
Practical Applications
Portfolio Management
Vomma analysis helps portfolio managers better understand the risk profile of their option positions, especially when dealing with large or complex portfolios that have significant exposure to volatility changes.
Option Spreads and Combinations
Traders can use Vomma to design and analyze option spreads and combinations that have specific volatility sensitivity profiles.
This allows for more precise control over a portfolio’s response to volatility changes.
Volatility Surface Analysis
Vomma helps when analyzing and constructing volatility surfaces, which are important for pricing and risk management across different strike prices and expirations.
Challenges & Limitations
Complexity
Vomma is a complex concept that requires a strong understanding of options theory and mathematics.
This complexity can make it challenging for less experienced traders to incorporate into their analysis and decision-making processes.
It requires software to compute.
Model Dependency
Like other Greeks, Vomma calculations are model-dependent.
Different option pricing models may produce slightly different Vomma values, which can lead to discrepancies in analysis and decision-making.
Market Liquidity Considerations
In less liquid options markets, the theoretical Vomma values may not accurately reflect real-world trading conditions, potentially leading to discrepancies between expected and actual outcomes.
Conclusion
Vomma is an advanced Greek used by options traders, market makers, and risk managers.
By providing insight into the second-order effects of volatility changes on option prices, it allows for more sophisticated analysis and decision-making in options trading and portfolio management.
Ultimately, Vomma serves as a reminder of the nuanced and non-linear nature of options pricing and risk.