Charm (Option Greek)

Charm, also known as delta decay or delta bleed, is one of the second-order Greeks used in options trading.
It measures the rate of change in an option’s delta with respect to time, assuming all other factors remain constant.
Understanding charm can help traders better manage their options positions and anticipate how their delta exposure may change as time passes.
Key Takeaways – Charm
- Charm predicts daily delta changes, important for accurate hedging.
- Monitor it closely, especially for at-the-money options near expiration.
- Weekend effect – Charm causes price gaps on Mondays. Adjust strategies accordingly, particularly for short-term options.
- Charm intensifies near expiration.
- Be prepared to manage positions more actively in the final weeks to avoid unexpected delta shifts.
The Basics of Charm
Definition
Charm is mathematically expressed as the partial derivative of delta with respect to time, which is the same as the derivative of theta with respect to the underlying price.
Charm = ∂Delta / ∂t = ∂θ / ∂S
It represents how much an option’s delta is expected to change each day as the option approaches expiration, all else being equal.
Interpretation
A positive charm indicates that the option’s delta is increasing over time, while a negative charm suggests the delta is decreasing.
The magnitude of charm indicates the rate of this change.
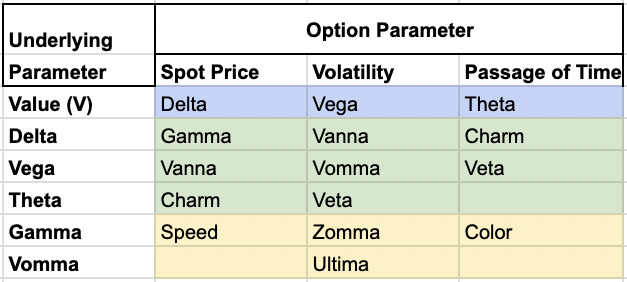
Factors Affecting Charm
Several factors influence an option’s charm:
Time to Expiration
Charm tends to be more pronounced as an option approaches expiration.
This is because the rate of change in delta accelerates as the time value of the option (theta) decays more rapidly.
Moneyness
At-the-money options typically experience the highest absolute charm values, especially near expiration.
In-the-money and out-of-the-money options generally have lower charm values.
Volatility
Higher implied volatility can lead to larger charm values, as it increases the uncertainty of the option’s final value at expiration.
Charm Behavior for Different Option Types
Call Options
For long call options:
- Out-of-the-money calls have negative charm
- At-the-money calls have charm close to zero
- In-the-money calls have positive charm
Put Options
For long put options:
- Out-of-the-money puts have positive charm
- At-the-money puts have charm close to zero
- In-the-money puts have negative charm
Practical Applications of Charm
Understanding charm can be valuable for options traders in several ways:
Delta Hedging
Traders who delta hedge their positions need to be aware of how their delta exposure changes over time.
Charm helps predict these changes, allowing for more accurate and efficient hedging strategies.
Weekend Effect
Charm is subject to the “weekend effect” in options trading.
Since time decay occurs even when markets are closed, options prices may gap at Monday’s open due to the accumulated charm effect over the weekend.
Position Management
By considering charm, traders can anticipate how their positions’ risk profiles will evolve.
This allows for more proactive management of their options portfolios.
Charm in Different Market Conditions
Steady Markets
In relatively stable market conditions, charm effects are often more predictable and easier to manage.
Volatile Markets
During periods of high volatility, charm effects can be more pronounced and less predictable, requiring closer attention from traders.
Limitations & Considerations
Charm has its limitations as a concept in options trading:
Model Dependency
Charm calculations are based on theoretical option pricing models.
These may not always perfectly reflect real-world markets.
Interaction with Other Greeks
Charm doesn’t exist in isolation.
Its effects interact with other Greeks, such as gamma and vega, which can complicate analysis and prediction.
Market Frictions
Transaction costs, bid-ask spreads, and other market frictions can make it challenging to capitalize on small changes in delta predicted by charm.
Advanced Charm Strategies
Experienced options traders may use more sophisticated strategies that leverage charm:
Charm-Neutral Portfolios
By balancing positions with positive and negative charm, traders can create portfolios that are relatively insensitive to the passage of time in terms of delta exposure.
Exploiting Charm Anomalies
Some traders attempt to profit from situations where the market may be mispricing options due to charm effects, particularly around weekends or holidays.
Charm’s Value to Market Makers
Charm is important for market makers because it helps them anticipate and manage daily changes in their delta exposure across their entire options inventory.
This allows them to adjust their hedges proactively, especially for at-the-money options near expiration.
Charm as a Source of Alpha
Capturing alpha from charm is extremely challenging. It requires:
- Real-time market-making capabilities to avoid bid-offer spreads
- Sophisticated multi-asset, tick-by-tick data processing
- Complex modeling of market participant behaviors, option mechanics, probability distributions and their higher-order moments
Sophisticated individual traders struggle to compete against high-frequency trading firms and market makers.
The alpha is volatile and heavily contested, making it nearly impossible for non-institutional players – discretionary, non-data-driven traders – to consistently profit from charm-related market movements.
Conclusion
Charm is a nuanced but important concept in options trading.
By understanding how delta changes over time, traders can make more informed decisions about position sizing, hedging, and risk management.
While charm alone shouldn’t drive trading decisions, incorporating it into a thorough analysis can potentially improve trading outcomes.
As with all aspects of options trading, it’s important to combine theoretical knowledge with practical experience and to adapt strategies to changing markets.
By mastering concepts like charm, traders can potentially improve their long-term performance.