Color (Option Greek)

Color, also known as gamma decay or DgammaDtime, is a concept in options trading, market making, and risk management.
It’s a third-order Greek measure that helps traders understand how the rate of change of an option’s Gamma varies over time.
Key Takeaways – Color (Option Greek)
- Color predicts daily Gamma changes, helping traders anticipate hedge effectiveness.
- Monitoring it can help maintain optimal risk exposure, especially for Gamma-hedged portfolios.
- Color intensifies near expiration, making Gamma more volatile.
- Hedges are adjusted more frequently as options approach maturity.
- At-the-money options typically have the highest Color values (common for many Greeks).
- We give an example of a Color trade below.
Definition
Color is defined as the third-order partial derivative of the option value with respect to the underlying asset price (twice) and time (once).
Mathematically, it’s expressed as:
Color = ∂Γ/∂𝜏 = ∂³V / (∂S² ∂𝜏)
Where:
- Γ (Gamma) is the rate of change of delta with respect to the underlying asset price
- 𝜏 (Tau) represents time to expiration
- V is the option value (sometimes represented with a C)
- S is the underlying asset price
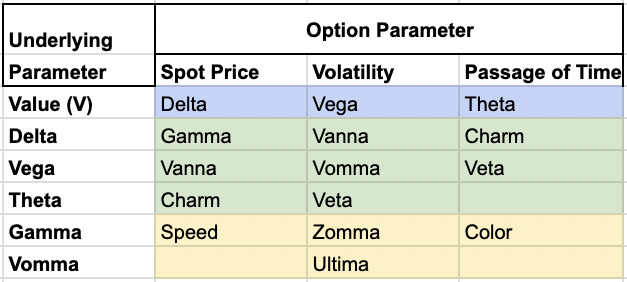
Relationship with Other Greeks
Color is closely related to other option Greeks:
Gamma
As color measures the rate of change of Gamma, it has a direct relationship with this second-order Greek.
Vanna
Vanna, which measures the rate of change of Delta with respect to volatility (or Vega relative to the spot price), is related to Color through their shared connection to Gamma.
Charm
Charm, or Delta decay, is another time-related Greek that often complements Color analysis in risk management strategies.
Greek Hierarchy
Let’s look at Color’s place in the hierarchy of option Greeks:
- First-order Greeks – Delta, Vega, Theta, Rho*
- Second-order Greeks – Gamma, Vanna, Charm, Vomma
- Third-order Greeks – Speed, Zomma, Color, Ultima
Color belongs to the third-order Greeks, which measure the rate of change of second-order Greeks.
*Rho is less common and not often listed on charts of the Greek sensitivities.
Importance of Color in Options Trading
Gamma-Hedged Portfolios
Color is important for traders maintaining Gamma-hedged portfolios.
These portfolios are designed to be neutral to small changes in the underlying asset price.
Nonetheless, as time passes, the effectiveness of this hedge can change.
Anticipating Hedge Effectiveness
By monitoring color, traders can anticipate how their Gamma hedge will perform over time.
This allows them to make proactive adjustments to their positions, maintaining the desired level of risk exposure.
Interpreting Color
Units and Scaling
The result of the color formula is expressed in Gamma per year.
However, traders often find it more practical to work with daily changes in Gamma.
Daily Color
To obtain the daily color, the annual color is typically divided by the number of trading days in a year (usually 252):
Daily Color = Annual Color / 252
This conversion provides a more intuitive measure of how Gamma is expected to change on a day-to-day basis.
Time Sensitivity
The accuracy of Color as a predictive tool depends on the time remaining until option expiration:
- Long-term options – Daily Color estimates are generally reliable when there’s a significant time until expiration.
- Near-term options – As expiration approaches, Color itself can change rapidly, making full-day estimates less accurate.
Factors Affecting Color
Several factors influence the value and behavior of Color:
Time to Expiration
As an option approaches expiration, color tends to increase in magnitude.
This reflects the accelerating rate of change in Gamma as time decay becomes more pronounced.
Underlying Asset Volatility
Higher volatility in the underlying asset can lead to more significant Color values, as it amplifies the potential for changes in Gamma.
Strike Price
The relationship between the option’s strike price and the current underlying asset price (moneyness) affects Color.
At-the-money options typically exhibit the most significant Color values.
Applications of Color in Risk Management
Dynamic Hedging
Color helps traders implement more sophisticated dynamic hedging strategies by anticipating changes in Gamma exposure in a position or the broader portfolio.
Portfolio Optimization
With Color analysis, portfolio managers can optimize their positions to maintain desired risk characteristics over time.
Options Pricing Models
Advanced options pricing models incorporate Color to improve the accuracy of valuations.
It’s most relevant for complex or long-dated options.
Trade Scenario: Delta-Gamma Neutral Portfolio Adjustment
Here, the trader looks to maintain a Delta-Gamma neutral position on a stock while anticipating changes in Gamma exposure due to time decay.
Step 1: Initial Position
- The trader has a Delta-Gamma neutral portfolio of options on XYZ stock.
- Current stock price = $100
- Portfolio – Long 100 ATM calls (strike $100), Short 10,000 shares of stock (100 shares per contract)
Step 2: Color Analysis
- The trader calculates the Color of their position.
- They find that the Color is -0.02 gamma per day.
- This indicates the portfolio will lose 0.02 in gamma exposure daily if unmanaged.
Step 3: Anticipating Gamma Change
- Over the next 5 trading days, the trader expects to lose 0.1 gamma (5 × -0.02).
- To maintain gamma neutrality, they need to adjust their position proactively.
Step 4: Position Adjustment
- To offset the expected gamma loss, the trader decides to buy 5 slightly OTM calls (strike $102).
- These new calls will provide the positive gamma needed to balance the decay.
Step 5: Monitoring and Fine-tuning
- The trader continues to monitor Color daily.
- They make small adjustments as needed to keep the portfolio Delta-Gamma neutral.
Step 6: Result
- By using Color, the trader maintains a more stable hedge over time.
- They avoid larger, more costly adjustments that would be necessary without this proactive approach – i.e., if Color were ignored in the analysis.
This trade demonstrates how Color helps options traders anticipate and smoothly manage changes in their portfolio’s risk exposures, particularly Gamma, as time passes.
It allows for more efficient hedging and potentially reduces transaction costs associated with larger, reactive position adjustments.
Limitations & Considerations
It’s important to understand Color’s limitations:
Model Dependency
Color calculations are based on theoretical option pricing models, which may not always perfectly reflect real-world markets.
Computational Complexity
Calculating Color requires complex mathematical operations, which can be computationally intensive for large portfolios.
Market Assumptions
The effectiveness of Color-based strategies depends on the validity of underlying market assumptions.
A lot of options theory from academic circles assumes continuous trading ample liquidity, and no transaction costs, which isn’t the case in real trading.
Conclusion
Color helps traders better understand their gamma exposure, and it enables traders to implement more sophisticated hedging and portfolio management strategies.
However, like all mathematical models in finance, it should be used in conjunction with other variables, parameters, sensitivities, analytical techniques, and market insights/signals for optimal decision-making.
Understanding and effectively using measures like color are important for traders and risk managers looking to maintain precise control over their positions and exposures.