Particle Filters in Finance & High-Frequency Trading

Particle Filters or Sequential Monte Carlo Methods – a Bayesian inference technique and machine learning algorithm – is increasingly relevant in quantitative finance and high-frequency trading (HFT).

This method employs a set of random samples, or “particles,” to approximate the posterior distribution of a stochastic process.

In the context of HFT, particle filtering can help track and predict the rapid changes in market prices and dynamics.

Key Takeaways – Particle Filters in Finance & High-Frequency Trading

• Technique for estimating the state of a system sequentially over time.
• Useful in situations where the system is non-linear and/or the state cannot be observed directly, which is common in high-frequency trading (HFT) scenarios.
• In HFT, particle filtering can be applied to estimate unobservable variables such as the intrinsic value of a security, market sentiment, or the actions of other traders, all of which are dynamic and evolve over time.
• We do a coding example and provide a diagram of particle filtering to help visualize the concept.

Particle Filters in HFT in Simple Terms

Imagine you have a bunch of little robots (particles) guessing where a balloon will go next as it bounces around a room.

Each robot makes a guess based on where it’s seen the balloon go before.

Over time, you trust the robots that guess right more often (i.e., up-weight their opinions) and down-weight the opinions of the ones that are usually wrong.

In HFT:

Prediction

Just like the robots predicting the balloon’s path, computers use particle filtering to predict asset prices’ movements very quickly.

Updating Beliefs

When new information comes in (like a change in stock price), the computer updates its guesses, giving more attention to the predictions that were closer to what actually happened.

Making Decisions

Based on these updated predictions, the algorithm quickly decides whether to buy or sell whatever it’s trading to make a profit.

Application in Market Dynamics Modeling

Tracking Market States

Particle filters enable the tracking of market states by representing the probability distribution of various market conditions.

It updates the distribution of these states as new market data arrives.

As such, it offers a real-time analysis tool.

Dealing with Non-Linearities and Non-Gaussian Noises

Financial markets often exhibit non-linear patterns and non-Gaussian noise, which traditional linear models can’t adequately address.

Particle filtering, with its non-parametric nature, excels in modeling these complexities.

Particle Filtering in Risk Management

Estimating Risk Measures

By simulating a wide range of market scenarios, it provides a probabilistic distribution of potential losses to enhance risk assessment accuracy.

Stress Testing

Stress testing is important for understanding potential extreme impacts.

Particle filtering helps in simulating extreme market conditions.

This helps traders and risk managers prepare for and mitigate these risks.

Algorithmic Trading Strategies

Predictive Modeling

Particle filtering aids in the development of predictive models for HFT.

Strategy Optimization

By simulating numerous trading strategies under different market conditions, particle filtering assists traders in identifying and optimizing strategies.

Particle Filter Coding Example

To understand how particle filters might be used in the context of high-frequency trading, let’s walk through the general steps of implementing a particle filter and then illustrate a simplified Python model.

We’ll also create a graph.

We think this’ll be helpful in visualizing what particle filtering is – i.e., actual value vs. estimated value – and how the estimated value tends to be smoother relative to the choppiness of the actual value.

An actual implementation in a high-frequency trading environment would need to be highly optimized and would involve more complex modeling of market conditions and participant behaviors.

HFT algorithms are also mostly implemented in C++ and not Python (because of speed), but that’s a different story.

General Steps of Particle Filtering

Initialization

Start with a set of particles (guesses) representing the possible states of the system.

Each particle has an associated weight indicating the probability that it represents the true state.

Prediction

Move each particle according to a predictive model. In the context of trading might be based on a combination of historical data, understanding of the cause-effect mechanics, and stochastic elements.

This prediction incorporates new information and evolves the state of each particle.

Update

When new data arrives (e.g., latest market prices, volumes, etc.), update the weights of the particles based on how well they predict the observed data.

Particles that are more consistent with the new data receive higher weights.

Resampling

Periodically, or when certain criteria are met, resample the particles to focus on areas of high probability.

Particles with higher weights are more likely to be selected during resampling.

Estimation

The estimate of the current state is derived from all particles and their weights, often as a weighted average.

Python Model

Below is a simplified Python model of a particle filter.

This model won’t directly apply to high-frequency trading but will give a conceptual understanding of how particle filtering works.

We’ll simulate a very basic one-dimensional random walk as the system we want to track.

import numpy as np
import matplotlib.pyplot as plt

# Number of particles
N = 1000

# Initial set of particles & weights
particles = np.random.normal(0, 1, N)
weights = np.ones(N) / N

# The "true" value to track
true_value = 0.5

# Store values for plotting
true_values = [true_value]
estimates = []

for t in range(1, 50): # Simulate time steps
true_value += np.random.normal(0, 0.1) # Update the true value
true_values.append(true_value)

particles += np.random.normal(0, 0.1, N) # Move particles

weights *= np.exp(-(particles - true_value)**2) # Update weights
weights /= sum(weights) # Normalize weights

indices = np.random.choice(range(N), N, p=weights) # Resampling
particles = particles[indices]
weights = np.ones(N) / N

estimate = np.sum(particles * weights) # Estimation
estimates.append(estimate)

# Plotting
plt.figure(figsize=(15,5))
plt.plot(true_values, label='True Value', color='blue')
plt.plot(estimates, label='Estimate', color='red')
plt.scatter(range(50), particles, color='green', s=1, alpha=0.3) # particle cloud
plt.title("Particle Filter Estimation Over Time")
plt.legend()
plt.xlabel('Time Step')
plt.ylabel('Value')
plt.show()

Particle Filter Visualization

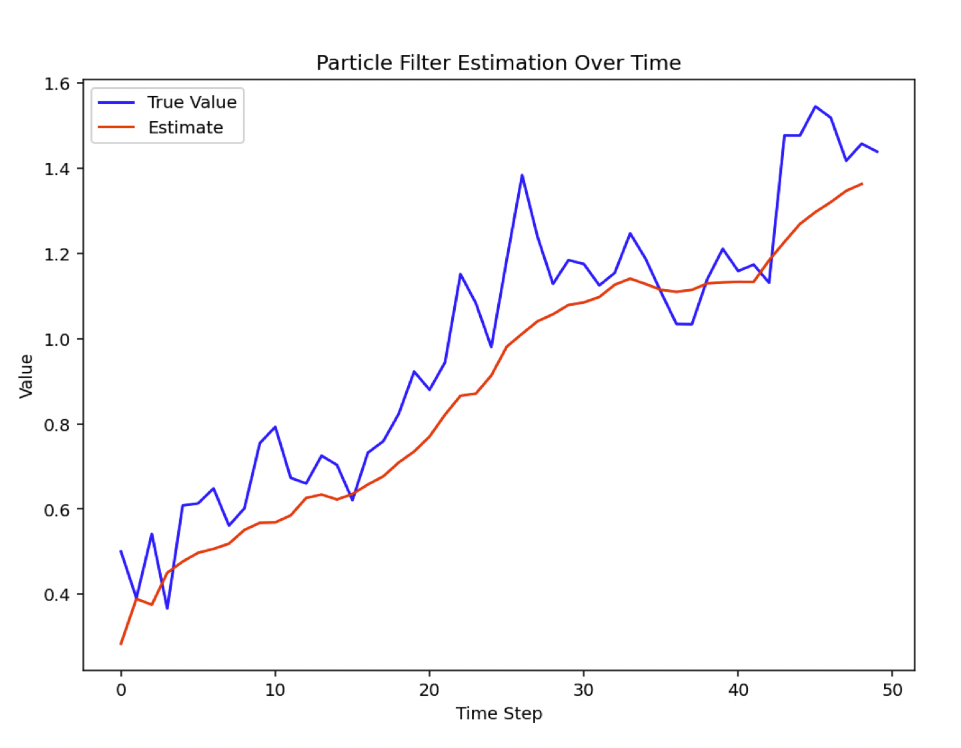
In this visualization:

• The blue line represents the true value of the system over time.
• The red line represents the estimate produced by the particle filter.

It might remind you of the concept of a moving average. We’ll cover the differences in the FAQ section toward the bottom of this article.

Note that if you use this code, please be sure to indent where appropriate given this is Python where indenting is an important part of the syntax.

Application in High-Frequency Trading

In a high-frequency trading scenario, particle filtering might be applied as follows:

• State Variables: The state might include various market indicators, the notional value of an asset, or hidden/unknown market factors.
• Prediction Model: This could be a complex model incorporating past price action, order flow data, or other market indicators.
• Observation Model: The actual market data observed in each time step, like price changes, volume, or trades.
• Resampling and Estimation: Focused on quickly and efficiently estimating the current state to make real-time trading decisions.

Particle filtering in HFT requires careful consideration of latency, data processing speed, and the stochastic nature of markets.

It’s often used in conjunction with other methods.

And it requires extensive testing and validation to ensure it’s adding value to the trading strategy.

Furthermore, due to the stochastic nature of financial markets, additional layers of risk management and anomaly detection are typically necessary when deploying these strategies live.

Can You Use Particle Filters in Other Forms of Trading and Investing Outside HFT?

Yes, particle filtering can be applied in various forms of trading and investing outside of HFT, given its ability to handle non-linear systems and non-Gaussian noise.

Risk Management

They can be used to model and predict complex risk factors dynamically.

This can help in stress testing and scenario analysis for managing portfolio risk.

Option Pricing

Particle filters can estimate the underlying dynamics of asset prices.

This is important in pricing options and other derivatives where the payoff depends on the stochastic evolution of underlying assets.

Economic Indicator Analysis

Investors and economists might use particle filters to estimate unobservable economic factors or to disentangle measurement errors from real economic signals in macroeconomic data.

Summary

In all these applications, the advantage of particle filtering is its flexibility to model non-linear relationships and evolve the state estimates dynamically as new data arrives.

Accordingly, it has value for various complex and time-varying financial systems.

Nonetheless, the effectiveness and efficiency of particle filtering in these contexts depend significantly on the:

• model specifics
• quality of the data, and
• implementation details…

…especially considering the computational cost and need for real-time processing in some trading scenarios.

Other Particle Filters

Each of these particle filters adapts or extends the basic particle filtering framework to better suit particular types of problems or to improve performance under certain conditions.

The field is evolving, with new variants and improvements being proposed to tackle increasingly complex and high-dimensional systems.

Adaptive Particle Filter

Adapts the number of particles during the filtering process to maintain a balance between computational efficiency and accuracy.

Auxiliary Particle Filter

Enhances the basic particle filter by selecting important particles based on an auxiliary variable, improving estimation in complex systems.

Block Particle Filter

Designed for high-dimensional state spaces by breaking down the estimation problem into smaller, more manageable blocks.

Cost Reference Particle Filter

Adapts the particle filter to minimize a cost function.

Typically used in control problems.

Dual Estimation Particle Filter

Simultaneously estimates the state of the system and unknown parameters or models.

Exponential Natural Particle Filter

Uses natural gradients in exponential families to update particles efficiently.

Most efficient in large-scale problems.

Feynman-Kac and Mean-field Particle Methodologies

Incorporate concepts from physics and mean-field theory for advanced particle approximations in complex dynamic systems.

Related: Feynman-Kac Formula in Finance

Gaussian Particle Filter

Approximates the posterior distribution with Gaussian particles.

Useful in mildly non-linear systems.

Gauss–Hermite Particle Filter

Employs Gauss-Hermite quadrature for better approximation in highly non-linear systems.

Hierarchical/Scalable Particle Filter

Structures particles in a hierarchical manner for scalable and efficient computations in large systems.

Multinomial Resampling Particle Filter

Uses multinomial sampling in the resampling step to choose the next generation of particles.

Nudged Particle Filter

Modifies standard particle filter by “nudging” particles towards high-likelihood areas to improve performance.

Particle Markov Chain Monte Carlo

Combines particle filtering with MCMC methods for enhanced sampling and inference in complex models.

Rao–Blackwellized Particle Filter

Reduces variance and computational load by analytically integrating out some variables.

Regularized Auxiliary Particle Filter

Adds a regularization step to the auxiliary particle filter for more stable and accurate estimations.

Rejection-sampling Based Optimal Particle Filter

Integrates rejection sampling to achieve optimal resampling in particle filters.

Residual Resampling Particle Filter

Combines deterministic and random components in the resampling step to reduce the variance of the weights.

Sequential Importance Resampling (SIR) Particle Filter

A fundamental type of particle filter that uses importance sampling and resampling to approximate posterior distributions.

Stratified Resampling Particle Filter

Improves the efficiency of resampling by ensuring a more uniform distribution of particles.

Swarm Particle Filter

Inspired by swarm intelligence, this filter uses collaborative particle behaviors to improve estimation.

Systematic Resampling Particle Filter

Ensures that particles are spread systematically over the entire range of the distribution for a more representative sample.

Transport Particle Filter

Incorporates optimal transport theory to guide the movement and selection of particles.

Unscented Particle Filter

Utilizes the unscented transform for better state estimation in highly non-linear systems.

FAQs – Particle Filter in HFT & Finance

What Is the Value of Particle Filters in Macroeconomics, Financial Mathematics, and Mathematical Finance?

Particle filters enable simulations to efficiently compute complex, high-dimensional integrals found in tasks like solving dynamic stochastic general equilibrium models in macroeconomics and pricing options – where traditional analytical or numerical methods may falter.

What Are Some Different Types of Particle Filters?

Other particle filters include:

• Adaptive Particle Filter
• Auxiliary particle filter
• Block Particle Filter
• Cost Reference particle filter
• Dual Estimation Particle Filter
• Exponential Natural Particle Filter
• Feynman-Kac and mean-field particle methodologies
• Gaussian particle filter
• Gauss–Hermite particle filter
• Hierarchical/Scalable particle filter
• Multinomial Resampling Particle Filter
• Nudged particle filter
• Particle Markov-Chain Monte-Carlo, see e.g. pseudo-marginal Metropolis–Hastings algorithm.
• Rao–Blackwellized particle filter
• Regularized auxiliary particle filter
• Rejection-sampling based optimal particle filter
• Residual Resampling Particle Filter
• Sequential Importance Resampling (SIR) Particle Filter
• Stratified Resampling Particle Filter
• Swarm Particle Filter
• Systematic Resampling Particle Filter
• Transport Particle Filter
• Unscented particle filter

Is a Particle Filter Like a Moving Average That Filters Signal from Noise?

A particle filter is somewhat analogous to a moving average in that both aim to discern signal from noise in financial data.

But particle filters are more sophisticated, handling non-linear and non-Gaussian (non-normal) problems by maintaining a set of hypotheses (particles) and updating them over time to represent the probability distribution of possible states.

This provides a dynamic, probabilistic estimate of financial variables or instrument prices.

Accordingly, it differs from the simpler trend-following mechanism of a moving average.

Conclusion

Particle filtering is a Bayesian filter used in high-frequency trading and other financial applications.

Particle filtering can handle non-linear dynamics, adapt to changing markets, and aid in risk management and strategy optimization.