Labor Productivity and Total Factor Productivity – Why They’re Important for Markets

Over the long run, an economy boils down to productivity.
When we trade markets and invest our money, our goal is to generate income. That income, over the long run, is a function of productivity and is the biggest driving force of economies over time.
In the near term, it’s economic cycles that make the biggest difference. But when all those even out over decades, it’s productivity that we’re left with as the thing that drives living standards forward.
If incomes didn’t grow faster than productivity and debts didn’t grow faster than incomes, then our large-scale economic problems (e.g., debt crises, booms and busts) would virtually never happen.
In this article, we’ll explore the topics of labor productivity and total factor productivity more deeply.
We’ll also consider how to calculate productivity as well as how to increase productivity.
Labor Productivity
Labor productivity is a function of the amount of output produced per hour worked.
You can calculate it by dividing an economy’s total output by the total number of hours worked across all workers.
For example, if an economy produces $500 billion in goods and services in a year and there are a total of 10 million people working an average of 2000 hours per year worked, then the labor productivity would be $25 per hour.
Productivity improvement
Increasing labor productivity is about producing more in the same amount of time or less or producing the same with less.
This is often done with technology or understanding how to do things better.
For repeatable tasks, a lot of machines have taken the work from humans.
Technological change
The first way to increase labor productivity is through technological change.
This is when we find new and better ways to produce things using the same or fewer inputs (labor, capital, land, etc.).
For example, imagine that it used to take 10 workers to produce 1,000 widgets per hour.
But then a new machine is invented that can do the work of those 10 workers in half the time.
Now the same 1,000 widgets can be produced in one hour with five workers.
The labor productivity has increased because we’re producing the same output with fewer inputs (labor).
Innovation and process improvement
The second way to increase labor productivity is by finding ways to do things better (i.e., innovation).
This is what’s known as process improvement and it usually comes about through experience and learning.
For example, imagine a company that makes custom furniture.
They might start out by taking a long time to make each piece of furniture.
But as they make more pieces, they’ll get better at it and be able to do it more quickly.
The same is true for any task that’s done repeatedly.
The more times you do it, the better you’ll become at doing it quickly and efficiently.
So, those are the two main ways to increase labor productivity: technological change and process improvement.
Copying as a means of process improvement
It’s also why people, companies, and countries tend to copy each other. It’s cheaper.
No one has to reinvent the wheel. Even in the investment industry, people build their portfolios in ways that build off what other investment managers have done.
For example, a mutual fund might track the S&P 500 because that’s a tried-and-true way to get exposure to large US companies and their overseas earnings in other markets.
And an exchange-traded fund (ETF) might track the S&P 500 because there’s already a basket of securities that’s been created and it’s easier (and cheaper) to just buy that than it is to create your own basket.
Back in the 1600s and 1700s, the English would copy Dutch ship making.
From there, they made process improvements and passed the Dutch in that domain in an era where ship making was a big part of overall economic progress, as it allowed them to bring their goods and currency all over the world.
China has copied a lot of US technology for the same reason.
Nonfarm Business Sector: Labor Productivity (Output per Hour) for All Employed Persons
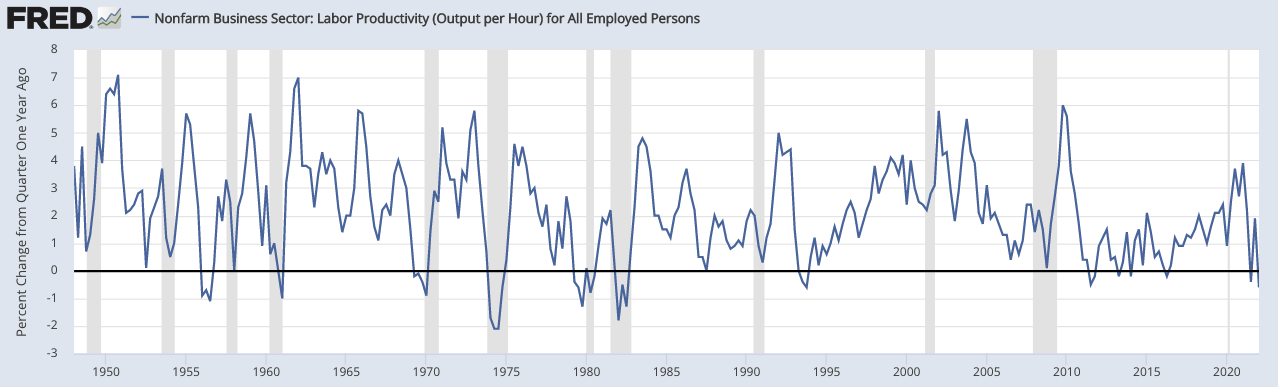
(Source: US Bureau of Labor Statistics)
Private Nonfarm Business Sector: Labor Productivity
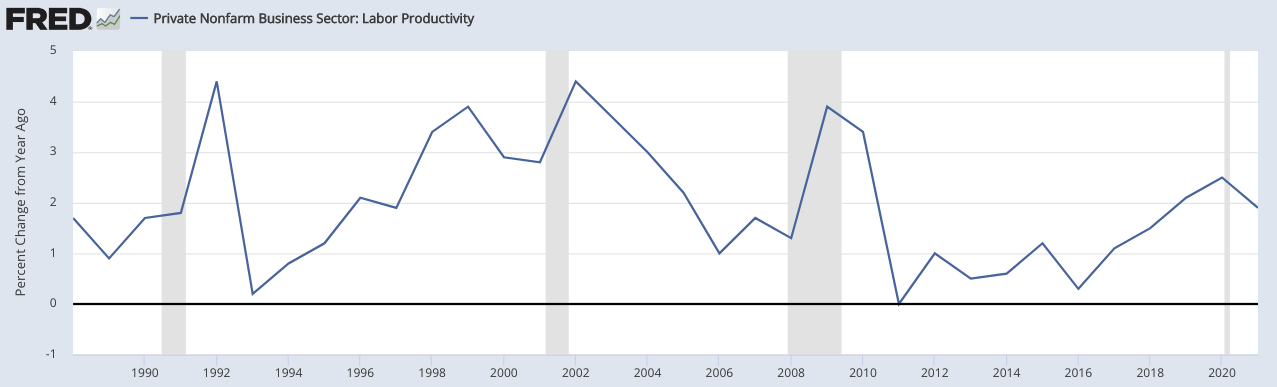
(Source: US Bureau of Labor Statistics)
Total Factor Productivity
Total factor productivity (TFP) is a measure of an economy’s efficiency in using all of its inputs (labor, capital, land, etc.) to produce output.
It’s calculated by dividing an economy’s total output by the combined inputs of all factors of production.
For example, if an economy produces $500 billion in goods and services in a year and the combined inputs of all factors of production are $400 billion, then the TFP would be 1.25.
An increase in TFP means that an economy is producing more with the same amount of inputs or the same amount with fewer inputs.
Increasing TFP usually comes about through technological change and/or process improvement, as we discussed with labor productivity.
Total Factor Productivity at Constant National Prices for United States
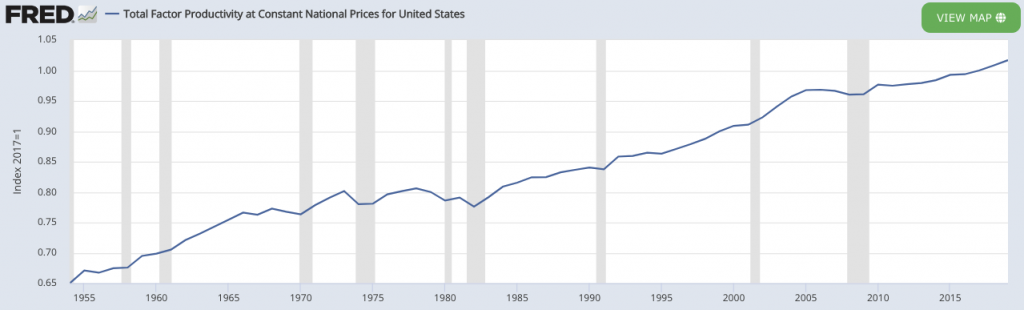
(Sources: University of Groningen; University of California, Davis)
How to calculate productivity
Money is used as a proxy for productivity, and money and credit growth is designed to track total trade, which is a function of productivity.
It’s not perfect, as the ebb and flow of credit creates economic cycles, but it does a good job.
People use money and credit to pay for things of value that were created by others, which in turn can be used to help them buy what they want.
Essentially goods and services are traded for goods and services, with money simply facilitating the process as a medium of exchange. Money can also be used as a store of value.
Their income, therefore, is a proxy for how productive they were within a certain amount of time.
On a per-hour basis, this might be expressed as how much they make per hour.
While countries may impose such things as minimum wage laws, a salary is only sustainable when their output is at least commensurate with the monetary value being paid.
In other words, a worker who gets paid $15 per hour needs to produce at least $15 worth of value in that hour.
If they don’t, the company will need to cover the loss, ask the worker to do more, or look to eliminate or reduce their labor needs in that area.
The same is true for a country as a whole. The only way a country can be sustainable over the long run is by producing more than it consumes.
It has to generate a surplus of output (or income) that it can then use to pay for what it needs and service its debt.
Multi-factor productivity
Multifactor productivity (MFP) measures economic performance by comparing the amount of output to the aggregate amount of combined inputs used to produce that output.
Inputs can include combinations of labor, capital, energy, materials, and purchased services.
Benefits of productivity growth
The benefits of productivity growth are many and varied, but they can be broadly grouped into three categories:
Increased output and incomes
When productivity grows, so does output. And when output grows, so do incomes.
With higher incomes, people can consume more goods and services, which raises their standards of living.
Increased employment
Productivity growth leads to increased output, which in turn leads to increased demand for labor.
This increased demand for labor can lead to higher employment levels, higher living standards, less social tension, more political cohesion, and so on.
Lower prices
Increased productivity often leads to lower production costs, which in turn leads to lower prices for consumers.
Lower prices allow consumers to purchase more goods and services, which raises their standard of living.
Business productivity
Business productivity is a measure of how well a company uses its resources to produce goods and services.
It’s calculated by dividing the company’s output by the inputs it uses.
For example, if a company produces $100 worth of goods and services in a year and it uses $50 worth of inputs, then its productivity would be 2.0.
More commonly, business productivity is expressed through margins. $100 of output with $50 of inputs would be considered a profit margin of 50 percent.
An increase in business productivity means that a company is able to produce more with the same amount of inputs or the same amount with fewer inputs.
Increasing business productivity usually comes about through technological change and/or process improvement.
Technological change can involve anything from developing new products and processes to improving existing ones.
Process improvement involves making changes to the way work is done to make it more efficient.
National productivity
National productivity is often defined as GDP (gross domestic product) as a whole, which includes the sales of new goods and services within a particular month, quarter, year, or other timeframe.
GDP per capita is used to how much output per person. Some countries might have lower GDPs but higher GDP per capita.
For example, the US has the world’s highest GDP at a national level but doesn’t have the world’s highest GDP per capita.
The following countries often have comparable or higher GDP per capita than the United States due to the particular idiosyncracies of these countries:
- oil and gas rich nations (Qatar, Norway, Kuwait, Brunei, UAE)
- tax havens (Ireland, Bermuda, Cayman Islands, Macau, Hong Kong, Singapore, Switzerland), and
- micro-states (Liechtenstein, Monaco, Luxembourg)
Reserve currency status and productivity
Reserve currency status has an effect on productivity because a global bias to hold one’s debt results in cheaper borrowing costs, which can yield a higher spread between ROI and interest costs.
This, in turn, leads to a better investment climate and higher productivity.
The United States has had the status of the world’s top reserve currency since the Bretton Woods Agreement in 1944.
This came to be when it appeared the US was destined to win World War II and the US had a monopoly on military and nuclear power, 80 percent of the world’s money (which was gold at the time), and 50 percent of the world’s output.
The Bretton Woods system broke down in 1971, but the dollar remains the world’s primary reserve currency.
Other countries with reserve currency status are:
- the euro (used by most of the European Union member states)
- the Japanese yen
- the British pound sterling
- the Swiss franc
- the Canadian dollar
- the Australian dollar
Productivity paradox
The productivity paradox is the observation that, despite all the advances in technology, we don’t necessarily have higher productivity rates.
There are a number of possible explanations for the productivity paradox:
Time for technology to mature
First, it takes time for people to learn how to use new technologies effectively.
It’s not enough to just have the latest gadgets and technologies; you need to know how to use them in order to see an increase in productivity.
For example, the metaverse is seen as a big technological advancement, but how much productivity is it generating? That’s a work in progress.
Some might even argue that certain applications of technology can lead to lower productivity, such as spending lots of time on social media, gaming, entertainment, and so on, even if it leads to higher productivity for the whole.
Difficult to measure some productivity in monetary terms
Second, many of the benefits of new technologies are non-monetary.
For example, consider the smartphone.
It’s hard to quantify the benefit of being able to instantly communicate with anyone, anywhere in the world. But it’s certainly not nothing.
The same goes for the internet, which has made a huge wealth of information available to anyone with a connection. It’s hard to put any type of exact dollar value on that, but it’s certainly valuable.
Indirect benefits
Third, there are often indirect benefits of new technologies that are hard to measure.
For example, the introduction of the automobile led to a boom in the tourism industry.
That’s not directly related to the productivity of cars, but it’s nonetheless a benefit that can be attributed to them.
Data lags
Fourth, there are often lags in the data that make it hard to see the impact of new technologies right away.
It can take years or even decades for new technologies to have their full effect on productivity. Consider the introduction of the steam engine in the late 18th century. It took many years for its full potential to be realized.
The same goes for the internet, which was introduced in the early 1990s but didn’t really take off until the late 1990s or early 2000s.
It’s only now that we’re starting to see its full effect on productivity and its numerous applications.
In sum, the productivity paradox is a real phenomenon, but it’s not necessarily a bad thing and shows how difficult it can be to measure productivity directly or understand long-run benefits.
New technologies often take time to mature and have indirect benefits that are hard to measure. Data lags can make it difficult to see the impact of new technologies right away, but over time, they can have a significant effect on productivity.
Productivity and Financial Markets
Productivity is ultimately what gives financial markets their real (i.e., inflation-adjusted) gains over the long run.
When we looked at the historical returns of financial assets, it’s productivity increases that help drive along the income they throw off.
A financial asset is simply a claim on future earnings (income), which is productivity.
So ultimately for financial assets to have value over time, they must contribute to increased productivity and evolution as a whole.
Productivity gains don’t just come from new technology, but also from things like improving work processes, organizational changes, and so on.
In sum, productivity is important for financial markets because it is the ultimate driver of real income growth, which is what gives financial assets their value over time.
Productivity – FAQs
What is labor productivity?
Labor productivity is a measure of economic performance that compares the output of goods and services to the input of labor.
It is typically expressed as a ratio or as a percentage change from a base year.
How do you calculate labor productivity?
There are various ways to calculate labor productivity, but the most common way is to divide the output of goods and services by the number of hours worked.
This will give you the average output per hour worked.
You can also use other measures of input, such as capital, instead of labor.
How does productivity affect markets?
Productivity is important for financial markets because it is the ultimate driver of real income growth, which is what makes financial assets have value over time.
What are some ways to increase productivity?
There are many ways to increase productivity, but some common ones include investing in and creating new technology, improving work processes, and making organizational changes.
It’s important to keep in mind that it can take time for these measures to have an effect on productivity.
How can I improve my productivity?
There are many ways to improve your productivity, but some common ones include investing in new technology, improving work processes, and making organizational changes.
It’s important to keep in mind that it can take time for these measures to have an effect on productivity.
What is the productivity paradox?
The productivity paradox is the phenomenon whereby new technologies often have indirect benefits that are hard to measure.
Data lags can make it difficult to see the impact of new technologies right away, but over time, they can have a significant effect on productivity.
The paradox is that even though we may not see the immediate benefits of new technologies, they can still be very beneficial in the long run.
What is total factor productivity?
Total factor productivity is a measure of economic performance that compares the output of goods and services to the combined inputs of labor and capital.
It is typically expressed as a ratio or as a percentage change from a base year.
How do you calculate total factor productivity?
There are various ways to calculate total factor productivity, but the most common way is to divide the output of goods and services by the sum of hours worked and capital input.
This will give you the average output per unit of input.
You can also use other measures of input, such as land or natural resources.
What is the difference between labor productivity and total factor productivity?
The main difference between labor productivity and total factor productivity is that labor productivity only takes into account labor input, while total factor productivity includes both labor and capital inputs.
Total factor productivity is typically a more comprehensive measure of economic performance.
Conclusion
Productivity is a key driver of economic growth and market performance.
There are many ways to improve productivity, but it can take time for these measures to have an effect. The productivity paradox is the phenomenon whereby new technologies often have indirect benefits that are hard to measure.
The impact of new technologies may not be seen right away, such as the advent of the world wide web in the early-90s and what it’s become today. But over time, they can have a significant effect on productivity.
Total factor productivity is a more comprehensive measure of economic performance than labor productivity and includes both labor and capital inputs.
Improving total factor productivity can be done in many ways, but some common methods include advances in technology or process improvements to make people inputs more effective.
It also causes labor systems to become more dynamic, to include not just people but also technology and automation.