Renewal Theory in Finance, Markets & Trading

Renewal theory is a branch of probability theory that deals with the times at which events recur.
It’s based on the study of stochastic processes and has found applications across various fields, including finance, economics, and trading.
In the context of finance and trading, renewal theory can offer frameworks for decision-making under uncertainty, especially in modeling and analyzing market events, trading strategies, and risk management.
Key Takeaways – Renewal Theory in Finance, Markets & Trading
- Models Event Occurrences
- Renewal theory helps in modeling the timing and frequency of financial events, like defaults or market cycles.
- Insights into patterns that repeat over intervals.
- Informs Risk Management
- By predicting the likelihood of event recurrence, traders can better prepare for and mitigate risks associated with rare or cyclical market events.
- Enhances Decision Making
- Understanding the statistical properties of event timings helps traders make informed decisions regarding entry and exit points, portfolio rebalancing, and strategic planning.
Key Concepts
Renewal Process
At the core of renewal theory is the renewal process, which models the occurrence of events over time.
In finance, these events could be stock price movements reaching a certain threshold, trades occurring, or economic cycles restarting.
Inter-Arrival Times
This refers to the time between consecutive events in a renewal process.
Understanding the distribution of these times can help in predicting the future occurrence of financial events.
Renewal Function
The renewal function gives the expected number of renewals (or events) in a given time period.
It’s used for estimating the frequency of market movements or trading opportunities.
Limit Theorems
As time progresses, certain properties of renewal processes stabilize.
For instance, the average rate of renewals converges to a constant under specific conditions.
This principle can be applied to long-term financial market predictions.
Math Behind Renewal Theory
Let’s briefly look at the math behind renewal theory:
Key Idea
Model random events that occur independently over time.
Main Variables
- N(t) = Number of events up to time t
- Xn = Time between (n-1)th and nth events
Key Assumptions
- {Xn} are IID (independent and identically distributed)
- Time scale resets after each event
Key Equation – Renewal Function
- m(t) = E[N(t)] = ∑_{n=0}^{∞} F^n(t)
Where F(t) is CDF of Xn and m(t) is the expected number of events by time t.
Analysis focuses on
- Distribution of waiting times Xn
- Asymptotic behavior as t → ∞
- Limit theorems (LLN, CLT) for N(t)
The math builds on probability theory and stochastic processes.
Overall, renewal theory provides a useful mathematical framework for studying random recurrence.
Applications of Renewal Theory in Finance, Markets, and Trading
Market Timing
Traders can use renewal theory to model the timing of market highs and lows, interest rate changes, or other economic indicators.
By understanding the distribution of event inter-arrival times, traders can better time their entry and exit points.
Risk Management
Renewal theory can help in quantifying the likelihood of extreme market movements or the failure rates of financial instruments.
Related: Extreme Value Theory
Trading Strategy Development
Strategies such as mean reversion and momentum trading can benefit from renewal theory by identifying statistical patterns in the occurrence of price movements.
Economic Cycle Analysis
Renewal theory can contribute to the modeling of economic cycles, including expansions and recessions, by treating the cycle restarts as renewal events.
How Traders Can Use Renewal Theory
Predictive Modeling
Traders can develop models based on historical data to predict future market events.
For instance, by analyzing the inter-arrival times of past stock price peaks, traders can estimate the likelihood of future peaks within certain timeframes.
Strategy Optimization
Renewal theory can help in optimizing trading strategies by identifying the probabilistic nature of trading signals and market events.
This can allow for dynamic adjustment of strategies based on the expected frequency of opportunities.
Stress Testing
Applying renewal theory in stress testing scenarios allows traders and financial institutions to assess the resilience of their portfolios against rare but impactful events, by simulating the occurrence of such events over long periods.
Algorithmic Trading
In algorithmic trading, renewal theory can be used to design algorithms that automatically adjust to the changing frequency and magnitude of price movements.
This can improve the adaptability and performance of automated trading systems.
Coding Example – Renewal Theory
To illustrate an example of renewal theory in financial markets using Python, we’ll simulate the occurrence of market events (e.g., reaching a certain stock price threshold) and calculate the expected number of events up to time ( based on the renewal function.
This simple example will use exponential distribution for inter-event times (common in renewal theory applications due to its memoryless property).
import numpy as np
import matplotlib.pyplot as plt
# Parameters
lambda_param = 0.1 # Rate parameter for the exponential distribution
time_horizon = 50 # Total time horizon to simulate
num_simulations = 10000 # Number of simulations to approximate E[N(t)]
# Simulate one sequence of inter-event times
def simulate_inter_event_times(lambda_param, time_horizon):
inter_event_times = []
total_time = 0
while total_time < time_horizon:
next_time = np.random.exponential(scale=1/lambda_param)
total_time += next_time
if total_time < time_horizon:
inter_event_times.append(next_time)
return inter_event_times
# Simulate N(t) for multiple simulations
def simulate_N_t(lambda_param, time_horizon, num_simulations):
event_counts = np.zeros(num_simulations)
for i in range(num_simulations):
inter_event_times = simulate_inter_event_times(lambda_param, time_horizon)
event_counts[i] = len(inter_event_times)
return event_counts
# Calculate E[N(t)] - Expected number of events by time t
event_counts = simulate_N_t(lambda_param, time_horizon, num_simulations)
expected_num_events = np.mean(event_counts)
print(f"Expected number of events by time {time_horizon}: {expected_num_events}")
# Plotting the distribution of N(t)
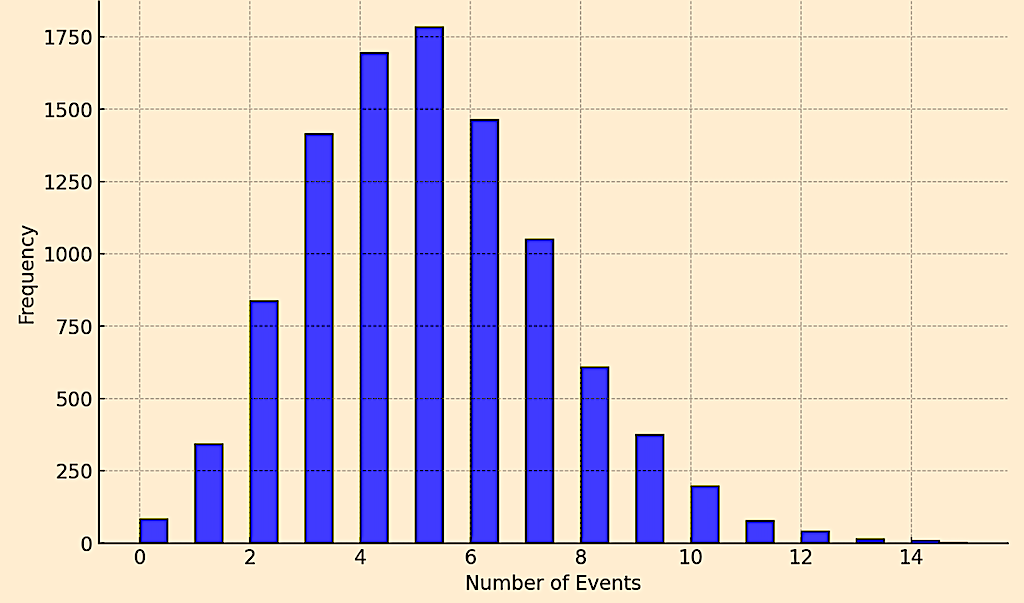
plt.hist(event_counts, bins=30, alpha=0.7, color='blue', edgecolor='black')
plt.title(f"Distribution of Number of Events by Time {time_horizon}")
plt.xlabel("Number of Events")
plt.ylabel("Frequency")
plt.show()
Explanation
- simulate_inter_event_times Function – Simulates the times between consecutive events (e.g., stock price reaching a threshold) using an exponential distribution.
- Stops once the cumulative time exceeds the time horizon.
- simulate_N_t Function – Repeats the simulation of inter-event times across multiple simulations to approximate the distribution of N(t), the number of events up to time (t).
- Expected Number of Events – Calculates the expected number of events up to time ( by averaging over all simulations.
Key Takeaways
- This code example uses the exponential distribution for inter-event times to model the occurrence of independent market events over time, in line with renewal theory principles.
- By simulating many sequences of events, we approximate the expected number of events E[N(t)] within a given time horizon.
- Provides insights into the frequency of certain market events.
- The histogram of across simulations gives a visual representation of how often specific numbers of events occur.
- Aids in any market analysis and risk assessment related to event frequencies.
Distribution of Numbers of Events by Time 50
Conclusion
Renewal theory is a framework for analyzing and making decisions in light of the stochastic nature of financial markets.
By leveraging the principles of renewal processes, traders and financial analysts can enhance their understanding of market dynamics/events/behavior, improve the timing of their trades, and refine their risk management practices.