Mutual Fund Separation Theorem

The Mutual Fund Separation Theorem (MFST) is a concept in portfolio theory that has impacted the way traders/investors approach portfolio construction and management.

The theorem posits that under specific conditions, market participants can optimize their portfolios by investing in a select number of mutual funds and risk-free assets, rather than purchasing a larger number of individual assets.

This approach offers numerous benefits, including reduced transaction costs and easier management of what they have in their portfolios.

Moreover, diversification reduces variance in outcomes, which can generally improve risk-adjusted returns (and often overall returns depending on how it’s done).

Below we look into the underlying principles of the Mutual Fund Separation Theorem, its advantages, and implications for the functioning of asset markets.

Key Takeaways – Mutual Fund Separation Theorem

• The Mutual Fund Separation Theorem (MFST) suggests that traders/investors can optimize their portfolios by investing in a select number of mutual funds and risk-free assets, rather than purchasing a larger number of individual assets.
• Investing in a smaller number of mutual funds offers benefits such as lower transaction costs, easier portfolio management, and enhanced diversification for better risk management.
• The MFST has implications for asset pricing models, facilitates passive investing through index funds and ETFs, and simplifies the process of building an optimal portfolio.

The Mutual Fund Separation Theorem: A Closer Look

The MFST relies on the notion that, under certain conditions, it’s possible to construct an optimal portfolio by investing in a smaller number of mutual funds and risk-free assets (e.g., cash, Treasury bills, government bonds) instead of a larger number of individual assets.

In this context, a mutual fund refers to any specified benchmark portfolio of the available assets.

These conditions typically involve assumptions about investor rationality, market efficiency, and the absence of taxes and transaction costs.

There are two primary advantages of the Mutual Fund Separation Theorem:

Lower transaction costs and easier management

When the relevant conditions are met, investing in a smaller number of mutual funds can be more cost-effective and less complex for investors.

Purchasing individual assets often involves higher transaction costs and requires more extensive research and monitoring.

By contrast, investing in mutual funds can provide diversification benefits and professional management at a lower cost.

Theoretical and empirical implications

The MFST offers valuable insights into the functioning of asset markets.

If it is assumed that the relevant conditions are indeed satisfied, researchers can derive and test hypotheses about market behavior, asset pricing, and portfolio management strategies.

This can lead to a better understanding of market dynamics and inform investment decisions.

Applications and Implications of the MFST

The Mutual Fund Separation Theorem has various applications and implications for both investors and financial markets:

Simplified portfolio construction

The MFST helps simplify the process of building an optimal portfolio.

By identifying the appropriate mutual funds, investors can achieve desired levels of risk and return without the need to analyze and invest in a large number of individual assets.

Enhanced diversification

Mutual funds provide investors with instant diversification by pooling their assets and investing in a diverse range of securities.

The MFST suggests that an optimal portfolio can be created by investing in a smaller number of these diversified funds, offering further benefits in terms of risk management.

It depends on the correlation between assets, but generally diversifying helps reduce risk without harming returns (up to a point where the benefits become increasingly marginal):

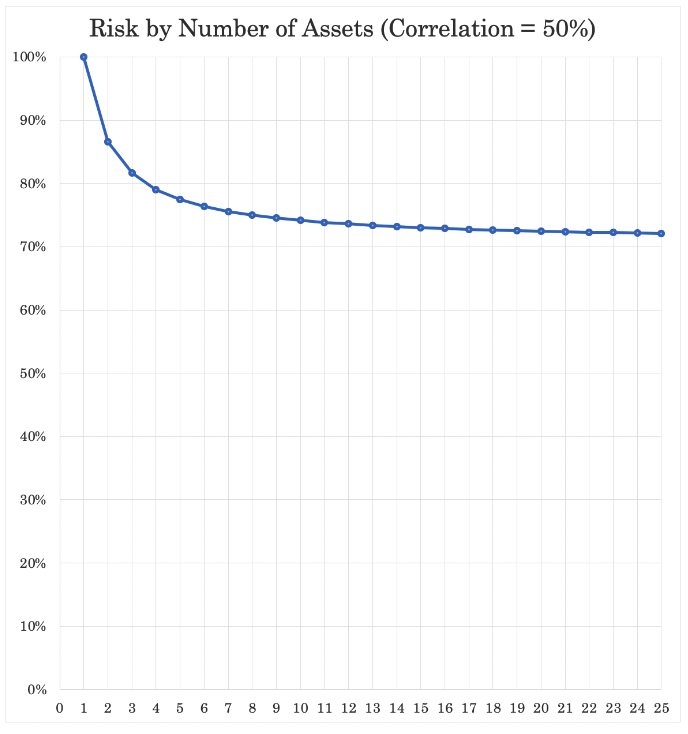
Facilitating passive investing

The MFST supports the idea of passive investing through index funds and exchange-traded funds (ETFs).

These funds replicate the performance of a specified benchmark or index, allowing investors to participate in market gains without the need for active management.

Implications for asset pricing models

The MFST has implications for the development of asset pricing models, as it suggests that optimal portfolio construction can be achieved using a smaller number of assets via pooled vehicles like mutual funds and ETFs.

This can lead to new insights into market behavior (e.g., more passive investment?).

FAQs – Mutual Fund Separation Theorem

What does the theorem imply about investor behavior?

The theorem suggests that all investors, irrespective of their risk tolerance, should hold the same portfolio of risky assets (in this case, a mutual fund) and differ only in the proportion they hold relative to risk-free assets.

This implies that the task of asset selection (choosing which specific stocks, bonds, etc., to hold) and asset allocation (deciding on the proportion of total wealth to invest in risky assets versus risk-free assets) can be separated.

How does the Mutual Fund Separation Theorem simplify investment decisions?

The theorem simplifies investment decisions by stating that investors only need to make two decisions:

• first, the choice of a mutual fund(s) that provide(s) the maximum return per unit of risk, and
• second, the division of their total wealth between this mutual fund (or mutual funds) and risk-free assets

This eliminates the need for each investor to analyze individual securities and commit to security selection.

Does the Mutual Fund Separation Theorem work in the real world?

The Mutual Fund Separation Theorem relies on certain assumptions, like the existence of a risk-free asset and the ability to lend or borrow at the risk-free rate.

In the real world, these assumptions may not hold true.

For instance, individual investors typically cannot lend at the risk-free rate.

Nonetheless, the theorem provides a useful framework to understand the relationship between risk and return, and serves as the foundation for many investment strategies.

How does the Mutual Fund Separation Theorem relate to Modern Portfolio Theory (MPT)?

The Mutual Fund Separation Theorem is an extension of MPT.

MPT introduces the concept of the Efficient Frontier, which represents the set of portfolios that offer the maximum possible expected return for a given level of risk.

The Mutual Fund Separation Theorem takes this a step further by identifying a single point (a mutual fund) on the Efficient Frontier that, when combined with a risk-free asset, can achieve any level of risk-return trade-off desired by the investor.

Can I implement the Mutual Fund Separation Theorem in my personal investment strategy?

While the assumptions of the theorem may not hold completely true in reality, its principles can guide personal investment strategies.

You can strive to identify a well-diversified mutual fund or set of funds (the “optimal risky portfolio”) that matches your risk-return expectations, and then determine your personal split between this fund and lower-risk assets based on your risk tolerance.

Are robo-advisors a practical application of the Mutual Fund Separation Theorem?

Yes, robo-advisors can be viewed as an application of the theorem.

They typically ask investors about their risk tolerance and financial goals, and then they allocate investments between a selection of risky assets (often in the form of ETFs or mutual funds) and risk-free or low-risk assets.

This mirrors the two key decisions in the Mutual Fund Separation Theorem.

How does the Mutual Fund Separation Theorem account for the different risk preferences of investors?

The theorem does not ignore risk preferences; instead, it includes them in the decision about the split between the risky mutual fund and risk-free assets.

A risk-averse investor would place a larger portion of their portfolio in risk-free assets, while a risk-seeking investor would invest more in the risky mutual fund.

The mutual fund itself remains the same in both cases.

Conclusion

The Mutual Fund Separation Theorem offers an approach to portfolio optimization, enabling traders/investors to achieve their financial goals more efficiently by investing in a select number of mutual funds.

This approach reduces transaction costs and simplifies investment management, while also providing insights into market dynamics and asset pricing.