Swap Pricing Models

Swap pricing models are used in the financial industry for valuing and managing interest rate swaps, currency swaps, commodity swaps, and other types of swaps.

These models help determine the fair value of swaps, which are agreements between two parties to exchange cash flows based on specified variables.

The complexity of swap contracts, which may involve exchanging fixed for floating interest rates, different currencies, or payments based on commodity prices, necessitates sophisticated pricing techniques.

Key Takeaways – Swap Pricing Models

• Interest Rate Models
  • Swap pricing heavily relies on interest rate models (like the LIBOR Market Model or the Black-Derman-Toy model) to forecast future interest rates and discount cash flows, which helps with determining the present value of swap payments.
• Credit Risk Assessment
  • The creditworthiness of the counterparties impacts swap pricing, as the perceived risk of default affects the swap’s cost or benefit.
  • Requires adjustments for credit risk, especially in credit default swaps.
• Market Expectations and Liquidity
  • Swap pricing is influenced by market expectations of future economic conditions and liquidity in the swap market, with tighter bid-ask spreads for highly liquid swaps and adjustments for illiquid or complex swaps.

Below are key concepts and types of pricing models commonly used in swap pricing:

Key Concepts

Net Present Value (NPV)

The fundamental concept in swap pricing is calculating the net present value of the cash flows exchanged in the swap.

This involves discounting future cash flows to their present value using an appropriate discount rate.

Discount Factors

These are used to calculate the present value of future cash flows.

The selection of discount rates is important and can be based on zero-coupon rates, SOFR, or other benchmark rates.

Forward Rates

Essential for pricing future cash flows, forward rates are determined based on current interest rates and the interest rate term structure.

Curve Construction

Interest rate curves (e.g., short-term interest curve, OIS curve) are used to derive discount factors and forward rates.

Building accurate yield curves is fundamental for pricing swaps.

Credit Risk

The creditworthiness of the counterparties affects swap pricing since it impacts the perceived risk of future cash flow payments.

Credit Valuation Adjustment (CVA) is a common method to account for this risk.

Comparative Advantage

Swaps often arise from the comparative advantage different parties have in different markets.

This principle, while more strategic than quantitative, underlies the reason swaps are beneficial.

Why Would Companies Engage in Swap Trading?

A classic example is a company based in the United States with a comparative advantage in obtaining USD financing at lower rates, while a European company has a similar advantage in the Eurozone for EUR financing.

By entering into a currency swap, both companies can access cheaper financing in their non-native currencies through the other party by leveraging their respective comparative advantages in their local markets.

Types of Swap Pricing Models

Black Model

Adapted from the Black-Scholes model for options pricing, the Black model is used for pricing interest rate caps, floors, and European swaptions.

As we covered in our swaptions pricing article, it’s useful for pricing swaptions as well.

LIBOR Market Model (LMM)

Also known as the BGM Model (Brace-Gatarek-Musiela model) – LIBOR itself was phased out back in June 2023 – this is used for pricing interest rate derivatives, including complex swaps and swaptions.

It models the evolution of the entire yield curve using a no-arbitrage approach.

Hull-White Model

A one-factor or two-factor interest rate model used to price interest rate derivatives, including swaps.

The Hull-White model can adapt to fit the current term structure of interest rates, which makes it versatile for pricing various interest rate derivatives.

Heath-Jarrow-Morton (HJM) Framework

A no-arbitrage model used to determine forward rates and thus price interest rate derivatives.

The HJM framework models the entire forward rate curve directly.

Monte Carlo Simulation

Monte Carlo Simulation in swap pricing involves using random sampling and statistical modeling to forecast the future cash flows and discount rates under numerous scenarios.

Provides a comprehensive range of potential outcomes and their probabilities to accurately assess the swap’s value.

Used heavily for pricing complex swaps that have path-dependent features or where analytic solutions aren’t feasible.

This numerical method simulates multiple scenarios of future interest rate paths to estimate the value of the swap.

Cross-Currency Swap Valuation Models

These models account for the exchange of interest payments in different currencies and use market data from both currencies’ yield curves for pricing.

Coding Example – Swap Pricing Models

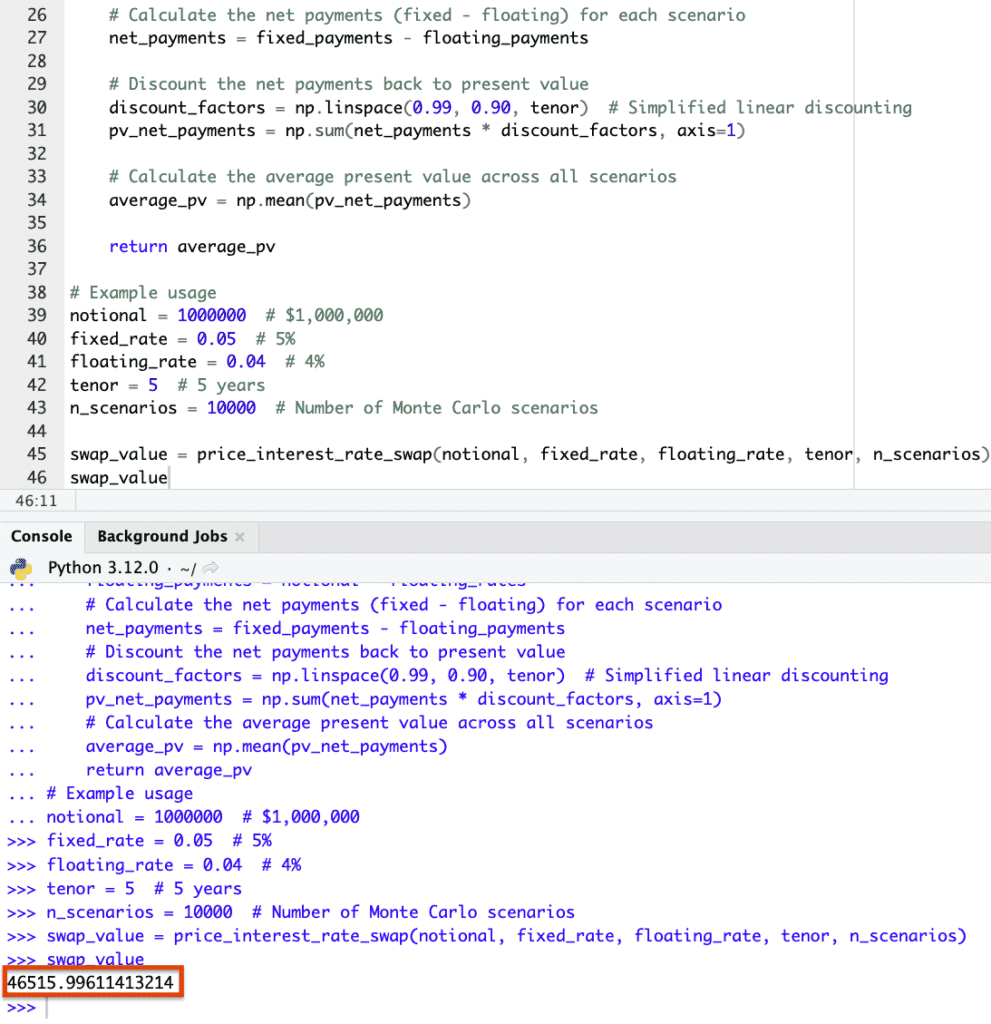
The example Python code for pricing an interest rate swap using a Monte Carlo simulation estimates the swap’s value to be approximately $46,516.

This simulation takes into account changes in the floating interest rate over the tenor of the swap under 10,000 different scenarios.

It compares these outcomes to the fixed payments to compute the average present value of the net payments.

import numpy as np

def price_interest_rate_swap(notional, fixed_rate, floating_rate, tenor, n_scenarios):
    """
    Simple example to price an interest rate swap using a Monte Carlo simulation.

    Parameters:
    notional: Notional amount of the swap.
    fixed_rate: Fixed interest rate of the swap.
    floating_rate: Initial floating interest rate of the swap.
    tenor: Total tenor of the swap in years.
    n_scenarios: Number of scenarios for the Monte Carlo simulation.

    Returns:
    Average swap value from the simulation.
    """
    np.random.seed(35)
    # Simulate floating rate changes over the tenor of the swap
    floating_rate_changes = np.random.normal(0, 0.01, (n_scenarios, tenor)) # Small vol assumption
    floating_rates = floating_rate + np.cumsum(floating_rate_changes, axis=1)

    # Calculate fixed payments and floating payments for each scenario
    fixed_payments = notional * fixed_rate
    floating_payments = notional * floating_rates

    # Calculate the net payments (fixed - floating) for each scenario
    net_payments = fixed_payments - floating_payments

    # Discount the net payments back to present value
    discount_factors = np.linspace(0.99, 0.90, tenor) # Simplified linear discounting
    pv_net_payments = np.sum(net_payments * discount_factors, axis=1)

    # Calculate the average present value across all scenarios
    average_pv = np.mean(pv_net_payments)

    return average_pv

# Example usage
notional = 1000000 # $1,000,000
fixed_rate = 0.05 # 5%
floating_rate = 0.04 # 4%
tenor = 5 # 5 years
n_scenarios = 10000 # Number of Monte Carlo scenarios

swap_value = price_interest_rate_swap(notional, fixed_rate, floating_rate, tenor, n_scenarios)
swap_value

Conclusion

Swap pricing models are used by financial institutions to manage risk and ensure that swaps are priced accurately according to market conditions.

The collection of models in this article provides a solid foundation for understanding the diverse methodologies applied in swap pricing.

The choice of model depends on the complexity of the swap, the variables involved, and the availability of market data.