1. Home

Master Equations in Finance

Contributor Image
Written By
Dan Buckley
Contributor Image
Written By
Dan Buckley
Dan Buckley is an US-based trader, consultant, and part-time writer with a background in macroeconomics and mathematical finance. He trades and writes about a variety of asset classes, including equities, fixed income, commodities, currencies, and interest rates. As a writer, his goal is to explain trading and finance concepts in levels of detail that could appeal to a range of audiences, from novice traders to those with more experienced backgrounds.
» Dan Buckley Profile Page
Updated
Dec 25, 2023

In finance, Master Equations are a set of mathematical tools used to model and understand various financial processes.

They mostly involve stochastic elements.

These equations are used in quantitative finance for modeling the dynamics of financial markets and instruments. 

They form the backbone of many advanced financial models, including those used for option pricing, risk management, and the valuation of derivatives.

 

Key Takeaways – Master Equations in Finance

  • Master Equations Represent Core Financial Dynamics:
    • In finance, master equations are mathematical formulations that capture the essence of financial processes
    • Example: The movement of asset prices or the evolution of interest rates over time.
  • Financial Modeling: 
    • These equations are useful for modeling/predicting future financial scenarios and analyzing market behaviors.
  • Basis for Advanced Financial Models:
    • Master equations form the backbone for more complex financial models used in risk management, portfolio optimization, and quantitative trading strategies.

 

Definition and Structure

A Master Equation typically describes the time evolution of the probability distribution of a stochastic process. 

For a financial variable X(t), the Master Equation might take a form such as:

 

∂P(x,t)/∂t = -∂/∂x [A(x,t) P(x,t)] + ½ ∂^2/∂x^2[B(x,t) P(x,t)]

 

Where:

  • P(x,t) is the probability density function of some variable (e.g., stock price)
  • X at time t and state x.
  • A(x,t) and B(x,t) are functions representing the drift (mean expected returns) and diffusion coefficients (volatility), respectively.

 

Applications in Finance

Option Pricing

The famous Black-Scholes equation for option pricing is a type of Master Equation.

It models how the price of an option evolves over time under stochastic asset dynamics.

Risk Management

Master Equations can model the evolution of risk factors and their impact on a portfolio.

It helps in the computation of Value-at-Risk (VaR) and other risk measures.

Market Dynamics Modeling

They are used to understand and predict market behavior.

Takes into account factors like volatility and market jumps.

Asset Pricing Models

In dynamic asset pricing, Master Equations help in understanding how asset prices evolve over time in response to various market factors.

 

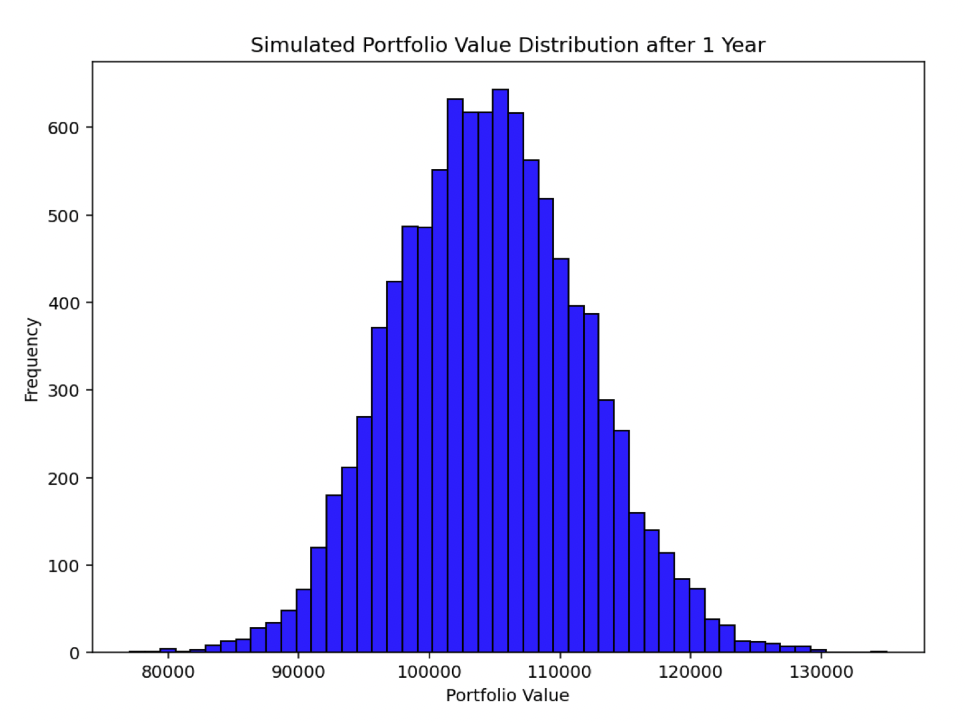
Monte Carlo Simulations

In practice, analytical solutions to Master Equations in finance are often intractable due to their complexity. 

This is where Monte Carlo simulations come in. 

They provide a numerical method to approximate the solutions of these equations by simulating a large number of paths for the stochastic processes and averaging the outcomes.

The result is a probability distribution of expected outcomes.

 

Probability Distribution
Probability Distribution

 

Conclusion

Master Equations enable the modeling of complex financial systems when their future state depends on probabilistic outcomes. 

Their applications range from pricing derivatives to managing portfolio risks.