Multicollinearity

What Is Multicollinearity?

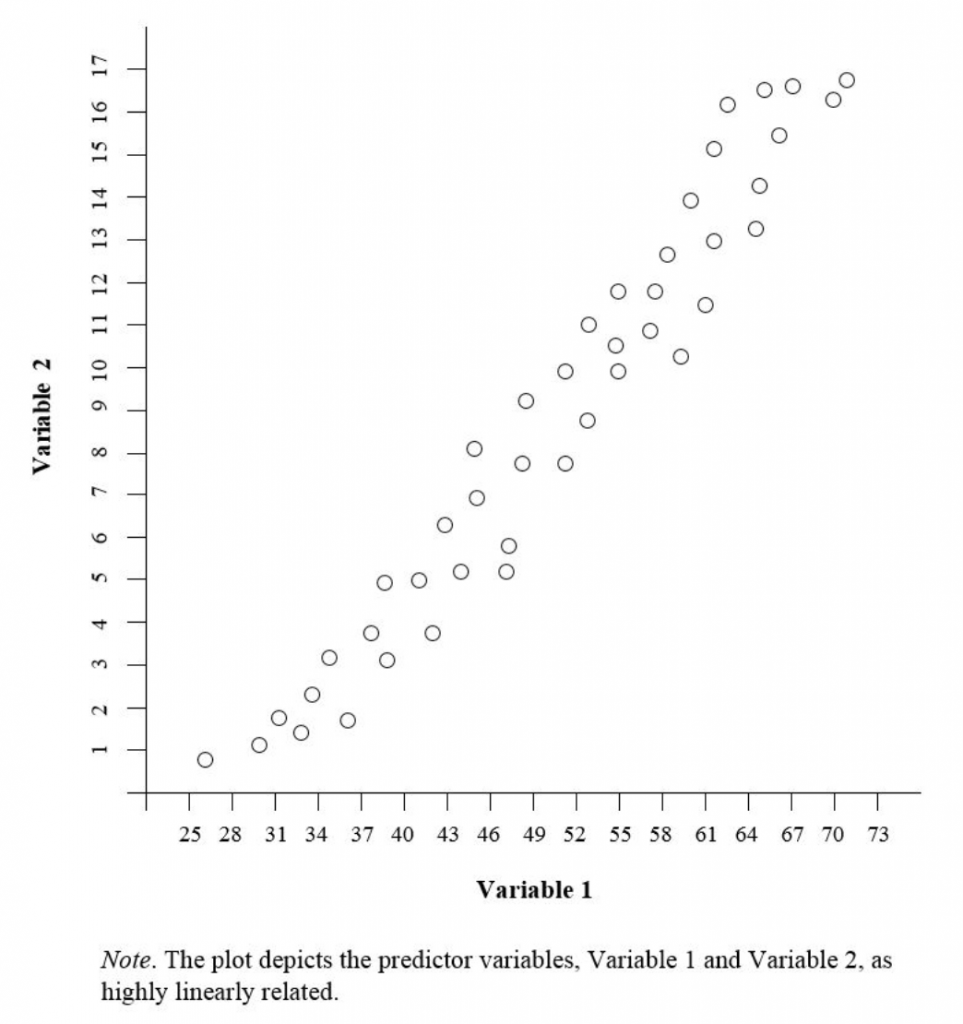
Multicollinearity occurs when two or more predictor variables in a regression model are highly correlated.

This correlation can cause problems with model estimation and interpretation.

When multicollinearity is present, the coefficient estimates for the individual predictors can be very sensitive to small changes in the data.

This means that the estimates may change drastically with even small changes in the data used to fit the model.

In addition, multicollinearity can make it difficult to interpret the individual coefficients because they no longer represent the unique contribution of each predictor variable.

All else being equal, multicollinearity also increases the standard errors of the coefficients, which makes it more difficult to assess their statistical significance.

Key Takeaways – Multicollinearity

• Multicollinearity occurs when independent variables in a regression model are highly correlated.
  • Leads to unreliable and unstable coefficient estimates.
• It inflates the variances of the coefficient estimates.
  • Makes it difficult to assess the effect of each variable on the dependent variable.
• Detection and remediation strategies include:
  • correlation matrices
  • variance inflation factor (VIF) assessment, and
  • removing or combining correlated variables

Understanding Multicollinearity

Multicollinearity is a common issue in regression analysis that can cause problems with model estimation and interpretation.

There are several ways to detect multicollinearity, and many methods for addressing it.

By understanding multicollinearity and taking steps to address it in your models, you can improve the accuracy and interpretability of your results.

How to Detect Multicollinearity

There are several ways to detect multicollinearity in a regression model.

One common method is to look at the correlation matrix of the predictor variables.

If there is high multicollinearity, the correlation coefficients will be close to 1 (or -1) for pairs of predictor variables.

Another way to assess multicollinearity is to look at the tolerance statistic.

Tolerance is the reciprocal of the variance inflation factor (VIF), which quantifies the amount of multicollinearity in a model.

A VIF of 1 indicates no multicollinearity, while values greater than 1 indicate increasing levels of multicollinearity.

A VIF that is close to 1 is not a cause for concern, but values greater than 5 or 10 may indicate multicollinearity that should be addressed.

Accepting a VIF less than 5 or 10 will depend on the number of explanatory variables involved.

A VIF above 5 will indicate severe collinearity when there are only two explanatory variables involved.

Finally, you can also look at the standard errors of the coefficients.

If multicollinearity is present, the standard errors will be large, which makes it more difficult to assess the statistical significance of the coefficients.

How to Address Multicollinearity

There are several ways to address multicollinearity in a regression model.

One common method is to simply remove one of the highly correlated predictor variables from the model.

Another approach is to use dimension reduction techniques such as principal component analysis (PCA) or partial least squares regression (PLS).

Both of these methods create new predictor variables that are linear combinations of the original predictor variables.

These new variables are called principal components or latent variables, respectively.

These methods can be used to reduce the dimensionality of the data while still retaining as much information as possible.

This can help to improve the interpretability of the coefficients and reduce the standard errors.

Finally, you can also use regularization methods such as ridge regression or lasso regression.

These methods penalize the size of the coefficients, which can help to reduce multicollinearity.

Multicollinearity (in Regression Analysis)

Example of Multicollinearity in Trading, Investing, and Financial Markets

The stochastic oscillator and Relative Strength Index (RSI) are two technical indicators that have similar inputs and thus produce similar outputs.

If you were to use both indicators in a trading or investing model, they would be highly correlated with each other and produce multicollinearity.

This would make it difficult to interpret the results of the model, as you wouldn’t know which indicator was responsible for the predictions.

In this case, it would be best to choose one of the indicators and remove the other from the model.

What Is Variance inflation factor (VIF)?

Variance inflation factor (VIF) measures the amount of multicollinearity in a set of multiple regression variables.

It quantifies the degree to which the inclusion of additional variables increases the variance of the coefficient estimates.

A VIF of 1 indicates no multicollinearity, while values greater than 1 indicate increasing levels of multicollinearity.

As mentioned above, a VIF that is close to 1 is not a cause for concern, but values greater than 5 or 10 may indicate multicollinearity that should be addressed, especially if there are a lower number of explanatory variables.

What is tolerance?

Tolerance is the reciprocal of the variance inflation factor (VIF), which quantifies the amount of multicollinearity in a set of multiple regression variables.

Tolerance can be used as a measure of multicollinearity in a multiple regression model.

Multicollinearity – FAQs

What are the consequences of multicollinearity?

Multicollinearity can have several consequences for a multiple regression model.

First, it can cause problems with model estimation.

If multicollinearity is present, the coefficients will be estimated with large standard errors, which means it will be harder to determine the statistical significance of the coefficients.

Second, multicollinearity can also cause problems with model interpretation.

If two or more predictor variables are highly correlated, it may be difficult to interpret the individual coefficients.

Finally, multicollinearity can also increase the chance of overfitting the model to the data. This can lead to inaccurate predictions on new data.

One common problem in trading and investing is fitting models based on past data, which invariably struggles when the future is different from the past.

Extrapolation can be dangerous, especially when models are overfitted and there isn’t the deep understanding of how the models are programmed.

How to detect multicollinearity?

There are several methods for detecting multicollinearity in a multiple regression model.

One common method is to look at the correlation matrix of the predictor variables. If two or more variables are highly correlated, this is a strong indication of multicollinearity.

Another method is to look at the condition index, which measures the linear dependence of the predictor variables. A high condition index indicates multicollinearity.

Finally, you can also look at the variance inflation factor (VIF), which quantifies the amount of multicollinearity in a set of multiple regression variables.

How to address multicollinearity?

There are several methods for addressing multicollinearity in a multiple regression model.

One common method is to use principal component analysis (PCA) or factor analysis to reduce the data’s dimensionality.

This can help improve the coefficients’ interpretability and reduce the standard errors.

You can also use regularization methods such as ridge regression or lasso regression. These methods cut down the size of the coefficients, which can help to reduce multicollinearity.

Finally, you can also choose to remove one or more of the predictor variables from the model if it just creates more of the phenomenon.

This may improve the interpretability of the coefficients, but it may also lead to a loss of predictive power with unaccounted variables that may be beneficial to be part of the model.

Summary – Multicollinearity

Multicollinearity is a common problem in multiple regression, where two or more predictor variables are highly correlated.

Multicollinearity can cause problems with model estimation and interpretation, and can also increase the chance of overfitting the model to the data.

There are several methods for detecting multicollinearity, including looking at the correlation matrix, the condition index, and the variance inflation factor (VIF).

There are also several methods for addressing multicollinearity, including using PCA or factor analysis, using regularization methods, or removing one or more predictor variables from the model.