Agent-Based Modeling (ABM) in Finance

Agent-Based Modeling (ABM) is a very important aspect of financial market analysis and prediction, but is one of the least talked about.

It operates under a different paradigm compared to traditional economic and financial models, which often rely on equilibrium theories (e.g., value investing, discounted cash flow) and aggregate market behaviors.

In ABM, the market is viewed as a complex system composed of various agents (individuals or entities) with distinct behaviors and interactions.

In reality, ABM is about:

• identifying the buyers and sellers
• estimating how much they’re likely to impact supply and demand
• how this picture changes based on variables that impact their actions (e.g., changes in discounted growth, discounted inflation, discount rates, risk premiums, regulation, and so on)

Under the ABM framework, it all comes down to who’s going to buy and who’s going to sell and for what reasons.

Key Takeaways – Agent-Based Modeling (ABM)

• Individual Agent Focus:
  • ABM in finance emphasizes the unique behaviors and interactions of individual market participants, rather than relying on aggregate market assumptions.
  • Who are the buyers and sellers? How big are they? What are they motivated to do?
  • Enables a more nuanced understanding of market dynamics.
  • Instead of considering “the market” to be a monolithic entity or basing decisions on notional equilibrium values, it’s about who’s buying and who’s selling and for what reasons.
• Data Intensity:
  • ABM requires extensive data on agent behaviors.
• Example:
  • We do a Python example of agent-based modeling later on in this article.

Key Components of Agent-Based Modeling in Financial Markets

Identification of Agents

This involves categorizing market participants as buyers or sellers.

Each agent is characterized by unique objectives, constraints, and decision-making processes.

In financial markets, these agents can range from individual investors and institutional traders to automated trading algorithms.

Agent Characteristics

Understanding the size and influence of each agent is crucial.

In financial markets, this might refer to the capitalization or trading volume controlled by an agent.

Larger agents (like institutional investors) can significantly impact market dynamics through their actions.

Agent Motivations and Behaviors

This is arguably the most complex aspect.

Agents’ decisions in financial markets are influenced by various factors, including, but not limited to:

Economic Indicators

Changes in macroeconomic factors like growth and inflation, often heavily viewed in the form of future expectations (discounted growth and inflation).

Discount rates and risk premiums also influence decisions.

Regulatory Environment

Changes in financial regulations can alter market dynamics.

Information Asymmetry and Market Signals

How agents interpret and react to market information.

Technological Changes

The impact of new technologies on market operations and strategies.

How Agent-Based Modeling Predicts Market Movements

Emergent Phenomena

Unlike traditional models, ABM can capture emergent phenomena – outcomes that arise from the interactions of individual agents but are not predictable from the characteristics of the agents themselves.

This includes market trends and bubbles.

Scenario Analysis

By simulating various scenarios considering different actions and reactions of agents, ABM can help in understanding potential future market movements.

Non-linear Dynamics

Financial markets are inherently non-linear; small changes can have disproportionately large effects.

ABM is well-suited to model these dynamics due to its focus on individual interactions.

Feedback Loops

ABM can incorporate feedback loops where the actions of agents influence the market, which in turn influences the agents, leading to complex dynamic patterns.

Challenges and Considerations

Model Complexity

ABMs can become exceedingly complex, requiring substantial computational resources – especially as the number of agents and the complexity of their interactions increase.

Data Requirements

Accurate modeling requires detailed data about agents and their behaviors, which can be difficult to obtain.

Parameter Sensitivity

ABMs can be sensitive to initial conditions and parameter choices, making them challenging to calibrate and validate against real-world data.

Agent-Based Modeling Example

To illustrate Agent-Based Modeling (ABM) in the context of the US Treasury market, let’s consider a simplified scenario with key agents categorized as buyers and sellers, along with their motivations.

Agents in the US Treasury Market

Sellers:

1. US Government: Issues Treasury bonds primarily to finance government spending.
2. Federal Reserve: May sell Treasuries as part of its monetary policy operations.
3. Individual Entities: Include private traders/investors, who may sell Treasuries for portfolio rebalancing or liquidity needs.

Buyers:

1. Pension Funds: Buy Treasuries for long-term income stability and to match their long-dated liabilities.
2. Commercial Banks: Purchase Treasuries as High-Quality Liquid Assets (HQLA) for regulatory liquidity requirements and for income.
3. Retail Investors: Attracted to Treasuries for their safety and income.
4. Hedge Funds: May buy Treasuries for strategic trading, hedging, or arbitrage opportunities.
5. Central Banks and Reserve Managers: Buy US Treasuries to manage foreign exchange reserves, often seeking safety and liquidity.

Modeling their Motivations and Interactions

Interest Rate Movements

A rise in interest rates might lead pension funds to increase their Treasury holdings for better yields, while hedge funds might engage in short-selling strategies anticipating bond price declines.

Economic Policy Changes

If the Federal Reserve signals tightening monetary policy, commercial banks might adjust their Treasury holdings in anticipation of changing liquidity environments.

Market Sentiments

In times of higher market volatility, traders might increase their Treasury holdings, seeking safety over higher returns.

Regulatory Changes

If regulatory requirements for HQLA are increased, commercial banks may respond by boosting their Treasury holdings.

Global Economic Factors

Central banks might adjust their Treasury investments in response to global economic conditions, affecting supply and demand dynamics.

Simulating Market Dynamics

Examples:

Scenario 1: Economic Downturn

In this scenario, retail and institutional investors might flock to Treasuries as a safe haven, driving up prices.

The Federal Reserve might add to this by buying Treasuries to inject liquidity into the market.

Scenario 2: Rising Interest Rates

This could lead to a sell-off in Treasuries, particularly by short-term investors and hedge funds.

Long-term holders like pension funds might be less reactive, considering their long-term income goals.

Scenario 3: Regulatory Shift

An increase in HQLA requirements could see a surge in demand from commercial banks, impacting Treasury yields and market liquidity.

Coding Example – Agent-Based Modeling

Let’s do an example.

In this simulation:

• Each agent has unique sensitivities to the economic factors and makes buy or sell decisions based on a weighted sum of these factors.
• Daily fluctuations in the economic factors are introduced, mimicking real-world variability.
• The collective decisions of all agents result in a net position each day, which influences the Treasury price.

The economic factors are discounted growth, discounted inflation, discount rates, and risk premiums. (Related: 4 Variables that Determine Financial Asset Pricing)

The Treasury price fluctuates in response to the aggregated decisions of the agents.

This demonstrates how individual behaviors and market conditions can impact financial instruments in a simplified ABM framework.

This Python model provides a basic understanding of how ABM can be used to study complex financial markets (albeit in a highly stylized manner).

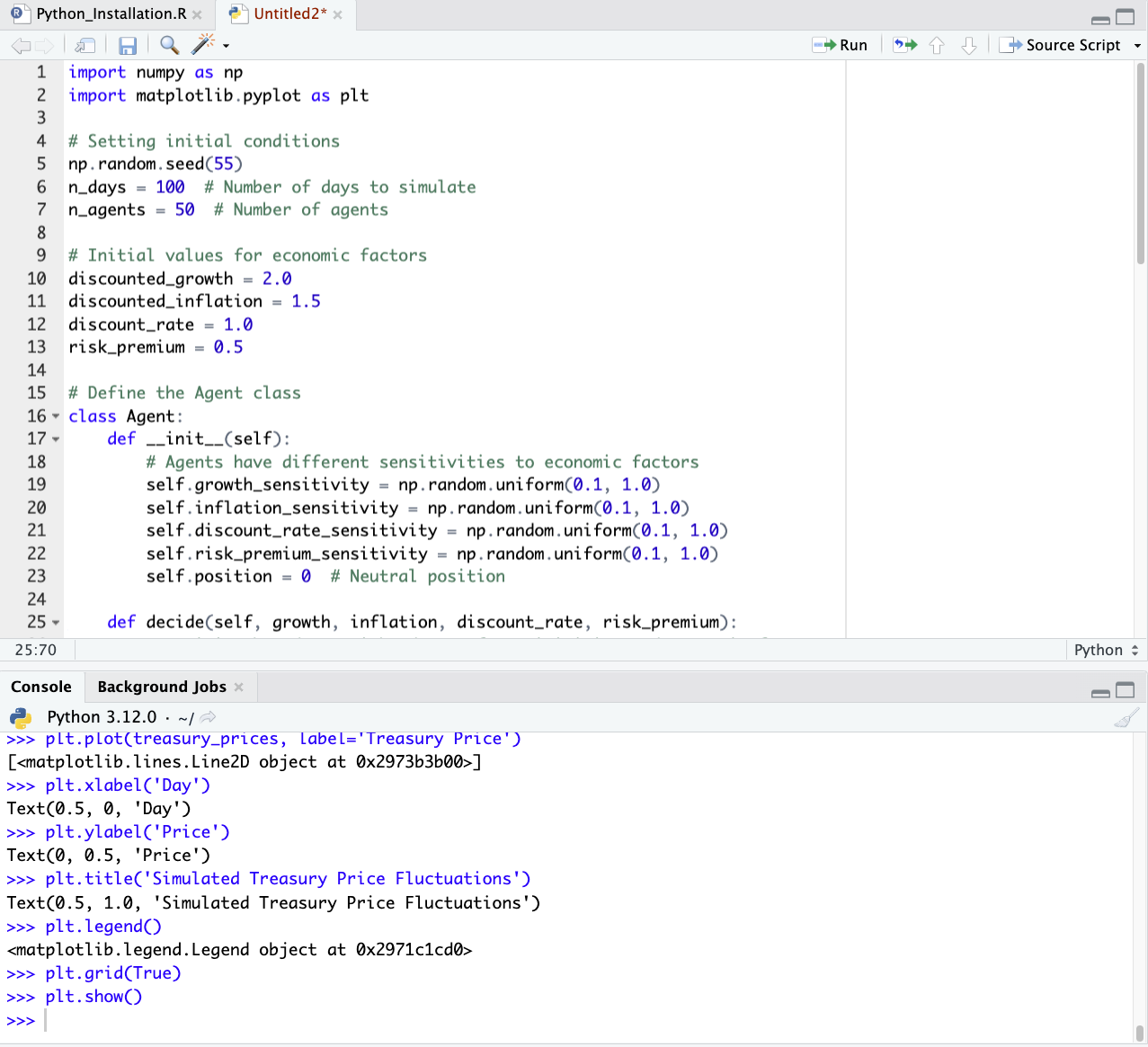
Agent-Based Modeling in Python

import numpy as np
import matplotlib.pyplot as plt

# Setting initial conditions
np.random.seed(55)
n_days = 100 # Number of days to simulate
n_agents = 50 # Number of agents

# Initial values for economic factors
discounted_growth = 2.0
discounted_inflation = 1.5
discount_rate = 1.0
risk_premium = 0.5

# Define the Agent class
class Agent:
def __init__(self):
# Agents have different sensitivities to economic factors
self.growth_sensitivity = np.random.uniform(0.1, 1.0)
self.inflation_sensitivity = np.random.uniform(0.1, 1.0)
self.discount_rate_sensitivity = np.random.uniform(0.1, 1.0)
self.risk_premium_sensitivity = np.random.uniform(0.1, 1.0)
self.position = 0 # Neutral position

def decide(self, growth, inflation, discount_rate, risk_premium):
# Decision based on weighted sum of sensitivities and economic factors
decision_score = (self.growth_sensitivity * growth 
- self.inflation_sensitivity * inflation 
- self.discount_rate_sensitivity * discount_rate 
+ self.risk_premium_sensitivity * risk_premium)
if decision_score > 0:
self.position += 1 # Buy or increase holding
elif decision_score < 0:
self.position -= 1 # Sell or decrease holding

# Initialize agents
agents = [Agent() for _ in range(n_agents)]

# Lists to store simulation results
treasury_prices = []

# Simulation loop
for day in range(n_days):
# Random fluctuation in economic factors
discounted_growth += np.random.uniform(-0.05, 0.05)
discounted_inflation += np.random.uniform(-0.05, 0.05)
discount_rate += np.random.uniform(-0.02, 0.02)
risk_premium += np.random.uniform(-0.02, 0.02)

# Agents make decisions
for agent in agents:
agent.decide(discounted_growth, discounted_inflation, discount_rate, risk_premium)

# Calculate net position of all agents
net_position = sum(agent.position for agent in agents)

# Adjust Treasury price based on net position
# Base price is 100, and each net position unit changes the price by 0.1
treasury_price = 100 + 0.1 * net_position
treasury_prices.append(treasury_price)

# Plotting the results
plt.figure(figsize=(12, 6))
plt.plot(treasury_prices, label='Treasury Price')
plt.xlabel('Day')
plt.ylabel('Price')
plt.title('Simulated Treasury Price Fluctuations')
plt.legend()
plt.grid(True)
plt.show()

If using this code, please be sure to indent as needed, as this is necessary in Python syntax:

At the end, we get a plot of the simulation:

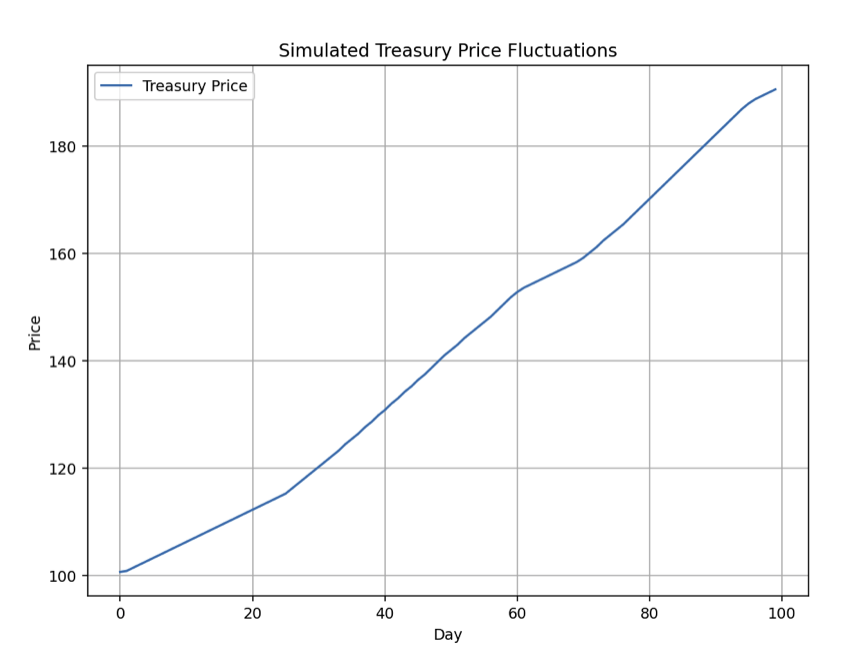
The plot above illustrates the simulated fluctuations in the Treasury price over a period of 100 days, based on the decisions of individual agents in response to changes in discounted growth, inflation, discount rates, and risk premiums.