Everything to Know About the Time Value of Money (TVM)

What Is the Time Value of Money?
The time value of money (TVM) is the concept that money you have now is worth more than the same amount of money in the future.
This is because the money that you have now can be invested and grow over time.
The time value of money is a basic principle of finance and has important implications for financial decision-making.
Why Does Time Value of Money Matter?
The time value of money is a very important concept in business and economics. It basically states that money today is worth more than money tomorrow (i.e., the future).
The reason for this is that money today can be invested and earn interest, whereas money tomorrow cannot. This concept is used in a variety of financial calculations, including the discounted cash flow (DCF) method.
The time value of money is also important for individuals to understand.
For instance, if you have $1,000 today, would you rather keep it or have $1,000 one year from now? Most people would prefer to have the money today so that they can invest it and earn interest on it.
There are a number of reasons why the time value of money is important.
First, it allows businesses to discount future cash flows in order to determine their present value. This is a vital part of investment decision-making.
Second, the time value of money can be used to compare different investments.
For example, if you have the choice between investing $1,000 in a stock or bond.
Which would you choose – the stock that will pay you $1,050 one year from now (based on its dividend) or a bond that will pay you $1,150 two years from now?
The answer depends on the discount rate.
If the discount rate is 5 percent, then the present value of the $1,150 bond is $1,043.08 (i.e., $1,150/(1+0.05)^2).
The present value of the stock would be $1,000 (i.e., $1,050/(1+0.05)^1).
This means that the bond is a better investment than the stock based on present value figured by a 5 percent discount rate, even though it will take two years to mature.
The time value of money is also important for individuals because it can help them make financial decisions.
For example, let’s say you have $10,000 in your savings account and you want to know whether you should keep it there or use it to pay off your credit card debt.
If the interest rate on your credit card debt is 15 percent and you get a low single-digit percentage on the savings account.
This means that paying off the debt may be a better use of your money than keeping it in savings, speaking in terms of what would save you the most money.
Of course, the time value of money is just one factor to consider when making financial decisions.
However, it is a very important concept that everyone should understand.
Formula for the Time Value of Money
The time value of money can be calculated using a simple formula:
FV = PV * (1 + r)^n
Where:
- FV = future value of money
- PV = present value of money
- r = interest rate per period
- n = number of years
Sometimes it’s written as:
FV = PV x [ 1 + (i / n) ] (n x t)
Where:
- FV = future value of money
- PV = present value of money
- i = interest rate per period
- n = number of compounding periods per year
- t = number of years
Time Value of Money Examples
To illustrate the time value of money, let’s say you have $1,000 that you want to invest.
You can either invest it now or wait a year and then invest.
Assume the rate of return is 10 percent per year.
If you wait a year to invest, the time value of money principle says that your $1,000 will be worth less than it is today.
This is because you could have invested the money a year ago and earned interest on it.
The time value of money formula can be used to calculate how much less your money will be worth in the future:
FV = PV * (1 + r)^n
- FV = $1,000 (1 + 0.10)^1
- FV = $1,000 x 1.10
- FV = $1,100
So, the time value of money principle says that your money will be worth 10 percent more in the future if you invest it now.
If you wait a year to invest, your money will only be worth the original amount plus interest.
The Time Value of Money and Discounted Cash Flow (DCF)
The TVM is central to DCF valuations.
In a DCF, you are projecting out a series of cash flows and discounting them back to the present by a certain interest rate.
The sum of these discounted cash flows gives assets their “present values” – i.e., their prices.
The time value of money is the mechanism that allows us to compare cash flows that occur at different points in time.
Without discounting, all cash flows would be valued equally regardless of when they occur.
For example, a cash flow today and a cash flow in 10 years would each be worth $1 if we didn’t discount them.
But since we can earn interest on money invested today, the present value of a future cash flow will be less than its face value.
This is why we need to discount future cash flows when doing a DCF analysis.
Discounted Cash Flow (DCF) Formula:
WACC * ((Future CF1 / (1 + r)^1) + (Future CF2 / (1 + r)^2) … + Terminal Value / (1 + r)^n))
Where:
- WACC = weighted average cost of capital
- r = discount rate
- CF = cash flow
- n = number of periods
The TMV is also an integral part of financial planning and risk management activities and DCF valuation is one aspect.
For example, pension funds will consider the TMV to ensure that their account holders will receive enough benefits in retirement.
Net Present Value
Net Present Value (NPV) is a widely-used financial metric that helps in evaluating the profitability of an investment or project.
It calculates the difference between the present value of cash inflows and the present value of cash outflows over a specific period.
NPV determines the net value created by an investment, taking into account the time value of money, which recognizes that a dollar received today is worth more than a dollar received in the future.
A positive NPV indicates that the investment is expected to generate more cash inflows than the initial investment cost, making it a potentially profitable opportunity.
Conversely, a negative NPV suggests that the investment may result in a net loss.
Decision-makers typically use NPV to compare different investment opportunities and select the one(s) with the highest positive NPV.
This approach is common in corporate budgeting.
Internal Rate of Return
The Internal Rate of Return (IRR) is a financial metric used to assess the attractiveness of an investment or project.
It represents the annualized rate of return at which the net present value of an investment becomes zero.
In other words, IRR is the discount rate that equates the present value of cash inflows with the present value of cash outflows.
A higher IRR indicates a more profitable investment, with the general rule being that an investment should be accepted if its IRR is greater than the required rate of return or cost of capital.
However, IRR has certain limitations, such as assuming that all cash flows are reinvested at the IRR itself, which may not always be realistic.
Modified Internal Rate of Return
The Modified Internal Rate of Return (MIRR) is a financial metric that addresses the limitations of the traditional Internal Rate of Return (IRR).
MIRR provides a more accurate measure of an investment’s profitability by incorporating the cost of capital and the reinvestment rate for cash flows.
MIRR calculates the return on an investment by assuming that all positive cash flows are reinvested at the project’s cost of capital, while all negative cash flows are financed at the project’s financing rate.
This approach provides a more conservative and realistic estimate of the investment’s profitability, making MIRR a better tool for decision-making when comparing investment opportunities.
Annuity
An annuity is a financial product that provides a series of periodic payments to an individual, usually for a specific period or over their lifetime.
Annuities are often used as a retirement planning tool, providing retirees with a steady income stream.
There are two main types of annuities:
- fixed
- variable
Fixed annuities guarantee a specified payment amount, while variable annuities’ payments are linked to the performance of an underlying investment portfolio.
Annuities can also be classified as immediate or deferred, depending on when the payments begin.
Immediate annuities start payments soon after the initial investment, while deferred annuities delay payments until a specified future date.
Perpetuity
Perpetuity is a financial concept that refers to an infinite series of cash flows paid at regular intervals (e.g., perpetual bonds).
In other words, perpetuity represents a constant stream of cash flows that continue indefinitely.
While true perpetuities are rare, they serve as a useful theoretical concept in finance and can be used to value certain types of assets or cash flow streams.
The present value of perpetuity can be calculated using a simple formula:
Present Value = Cash Flow / Discount Rate
This formula assumes that the cash flows remain constant over time, and the discount rate represents the time value of money.
Perpetuities can be used to value assets like preferred stocks, which pay a fixed dividend for an indefinite period, or to estimate the terminal value in a discounted cash flow analysis.
Why Are the Important Takeaway Concepts of the Time Value of Money?
The time value of shows a few important things:
“A dollar today is worth more than a dollar tomorrow”
The sooner you start saving/investing, the more time your money has to grow. Investing early can be crucial to building wealth over time.
These are important things to remember when making financial decisions.
For example, if you’re trying to decide whether to save for retirement or take a vacation, the time value of money can help you make the right decision.
If you’re trying to decide whether to buy a new car or invest in a portfolio, the time value of money can again help you make the right decision.
Delayed gratification
Delayed gratification is often key to success when it comes to personal finance.
The less you spend on normal items, the more you can save and invest.
Opportunity cost
The time value of money also takes into account opportunity cost, which is the cost of not investing your money. This is because it’s not earning a return.
For example, if you have $1,000 and don’t invest it, the opportunity cost is the potential earnings you could have made if you had invested the money.
Assuming a 10 percent annual return, the opportunity cost of not investing $1,000 for one year is $100.
Time Value of Money (TMV) – FAQs
What Is the Difference Between Present Value and Future Value?
The time value of money (TMV) is the difference between present value and future value.
Present value is the current worth of a future sum of money or stream of cash flows given a specified rate of return. Future value is the opposite, it is the sum of money that an investment will be worth at a specific time in the future.
How Does the Time Value of Money Work?
The time value of money is based on the premise that money today is worth more than money tomorrow.
This is because money today can be invested and earn a return, whereas money tomorrow (i.e., earned in the future) cannot.
What Is an Example of Present Value?
The present value of a future sum of money is the value today of receiving that future sum.
In other words, it’s the amount you would need to invest now in order to have a certain amount of money at a future date.
For example, let’s say you want to have $100,000 five years from now.
How much would you need to invest today in order to have that much money five years from now? The answer depends on two things: the interest rate and the length of time you have to invest.
If the interest rate is 5 percent, then you would need to invest $$78,352.62 today in order to have $100,000 five years from now.
That’s because your investment will grow at 5 percent per year (compounded), so after five years it will be worth $100,000.
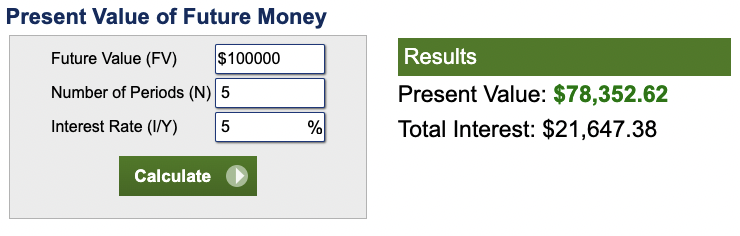
But what if the interest rate is 10 percent? In that case, you would only need to invest $62,092.13 today in order to have $100,000 five years from now.
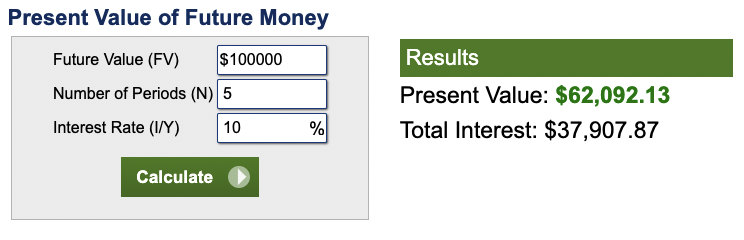
That’s because your investment will grow at a higher rate, so it will be worth more in the future.
What Is an Example of Future Value?
The future value of money is the amount of money that a sum of money will be worth at a specific point in the future, based on an interest rate.
For example, if you have $100 today and you expect to earn 5 percent interest on it each year, then in one year you will have $105.
In two years you will have $110.25, and in three years you will have $115.76. This process of earning interest on a sum of money is called compounding, and it is the key to growing your money over time.
The future value of money is important to understand because it can have a big impact on your finances.
For example, if you are saving for retirement, you need to know how much money you will need to have saved in order to live comfortably in retirement.
The sooner you start saving, the more time your money has to grow, and the easier it will be to reach your goal.
To calculate the future value of money, you need to know three things:
- the present value (the amount of money you have today)
- the interest rate, and
- the number of years you expect to earn interest
You can use an online calculator to do the math for you, or you can use the following formula:
Future Value = Present Value x (1 + Interest Rate)^Number of Years
For example, if you have $100 today and you expect to earn 5% interest each year for 10 years, your future value would be $162.89.
If you are saving for retirement, it is important to start as early as possible. The earlier you start, the more time your money has to grow.
For example, if you start saving at age 25 and contribute $200 per month until age 65 and earn 5 percent compounded annually, you will have $297,713.
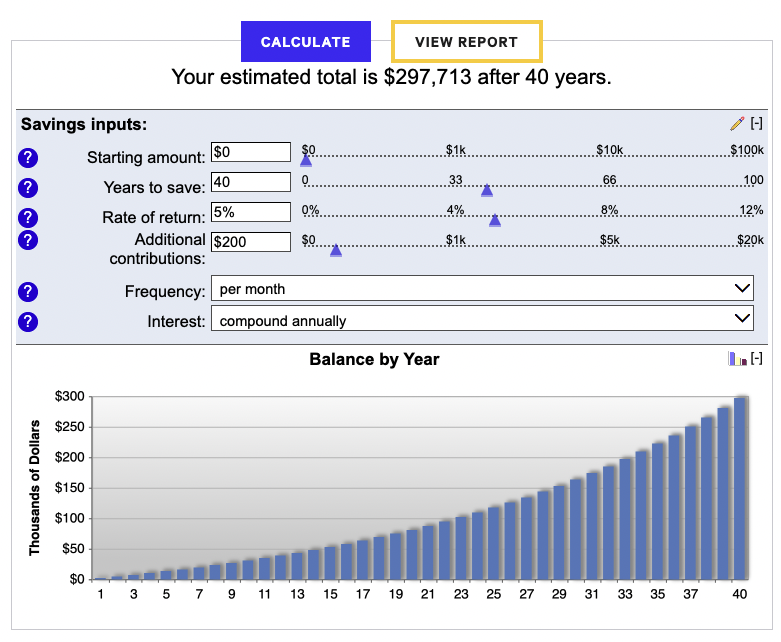
Summary – Time Value of Money (TMV)
The time value of money is the idea that money that is available today is worth more than the same amount of money in the future.
This is because money that is available today can be invested and earn a return, while money that is not available today cannot.
By understanding the time value of money, you can make better decisions about investing, saving, and spending.
For example, if you are saving for retirement, you should start as early as possible so that your money has more time to grow.
You can calculate the time value of money using a simple formula that takes into account the present value, interest rate, and number of years. Or you can use an online calculator.