Semivariance in Trading (Calculation, Application, Python Implementation)

Semivariance is a statistical measure used in finance to assess the downside risk of an investment or portfolio.

Unlike variance, which considers both upside and downside volatility, semivariance focuses solely on the negative variation of returns.

It provides a more targeted measure of risk that is particularly relevant for risk-averse investors.

Key Takeaways – Semivariance

• Risk Measurement: Semivariance concentrates on negative returns.
  • Offers a more targeted measure of downside risk than traditional variance.
• Asymmetry in Returns Analysis: It captures the asymmetry in return distributions, emphasizing losses.
• Portfolio Optimization: Semivariance helps in constructing portfolios that minimize the probability of large losses.

Semivariance – Calculation & Formula

Calculating semivariance involves a few steps, focusing specifically on returns that fall below a certain threshold, typically the mean or a target return.

Here’s the process laid out:

Define the Threshold

Decide on the threshold return level. This is often the mean of the returns, but it can be any benchmark or target return.

Collect Return Data

Gather historical return data for the asset or portfolio.

Isolate Returns Below Threshold

Identify all the returns that are less than the threshold.

Calculate Squared Deviations for Below-Threshold Returns

For each return below the threshold, calculate its deviation from the threshold.

Square each of these deviations.

Average the Squared Deviations

Add up all the squared deviations and divide by the number of below-threshold returns.

This average is the semivariance.

Formula Representation

Mathematically, if Ri​ represents individual returns and $T$ is the threshold, the semivariance is calculated as:

Semivariance = 1/N * ∑ Ri​<T ​(T−Ri​)^2

Lower Partial Variance

Semivariance is often referred to as Lower Partial Variance, emphasizing its focus on the lower, or negative, deviations from the mean or target return.

Significance

Downside Risk

Semivariance offers a more accurate measure of downside risk compared to total variance, which considers all volatility as equal.

Investment Analysis

It’s most useful for risk-averse investors or those with asymmetric risk tolerances, as it provides a clearer picture of the potential for losses.

Portfolio Construction

Understanding the semivariance of assets can aid in constructing portfolios that minimize the potential for downside losses.

Applications

Risk Assessment

Semivariance is used to evaluate the risk profile of individual securities or portfolios.

It focuses specifically on the likelihood and magnitude of negative returns.

Performance Evaluation

In conjunction with other metrics, semivariance can help assess the performance of portfolio managers, especially those who claim a focus on downside risk management.

Asset Allocation

Investors might use semivariance to inform their asset allocation decisions, choosing assets or asset classes with lower semivariance to reduce potential losses.

Advantages

Targeted Risk Measure

By focusing exclusively on negative returns, semivariance provides a more relevant risk measure for investors primarily concerned with downside.

Investor Preferences

Semivariance aligns well with the actual preferences of many investors, who often exhibit greater sensitivity to losses than gains.

Limitations

Ignores Positive Volatility

Semivariance does not account for the full range of an asset’s volatility, potentially overlooking important aspects of its risk profile.

Data Sensitivity

Like other statistical measures, semivariance is sensitive to the time period and frequency of the return data used in its calculation.

Calculation Complexity

The calculation of semivariance is more complex and data-intensive than standard variance, which might limit its use among some investors.

Python Code – Semivariance

To calculate semivariance in Python, we’ll follow the steps outlined previously.

For this example, let’s assume you have a list of returns and you want to calculate the semivariance relative to their mean.

Here’s a Python function that accomplishes this:

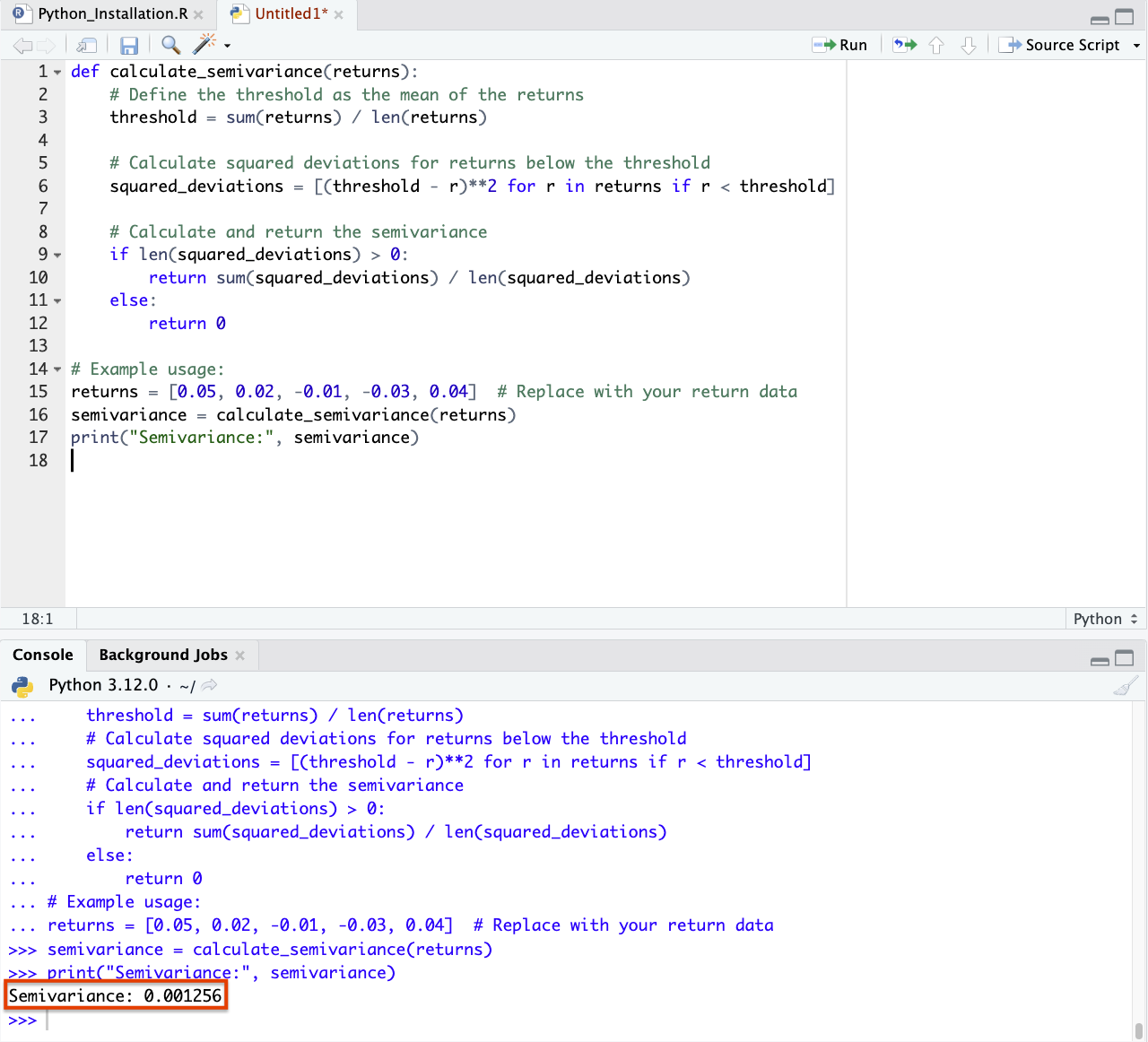
def calculate_semivariance(returns):
# Define the threshold as the mean of the returns
threshold = sum(returns) / len(returns)

# Calculate squared deviations for returns below the threshold
squared_deviations = [(threshold - r)**2 for r in returns if r < threshold]

# Calculate and return the semivariance
if len(squared_deviations) > 0:
return sum(squared_deviations) / len(squared_deviations)
else:
return 0

# Example use
returns = [0.05, 0.02, -0.01, -0.03, 0.04] # Replace with your own return data
semivariance = calculate_semivariance(returns)
print("Semivariance:", semivariance)

Given this is Python, please be sure to indent like as shown below. (Indentation is used to define the structure and scope of code blocks – i.e., logical grouping and execution sequence of code statements – such as those in loops, conditionals, and function definitions.)

In this function:

• The threshold is set as the mean of the provided returns.
• We use a list comprehension to calculate the squared deviations for each return below the threshold.
• The semivariance is then computed as the average of these squared deviations. If there are no returns below the threshold, the semivariance is set to zero to avoid division by zero errors.
• You can use this function with any list of returns to compute their semivariance.

Conclusion

Semivariance offers a more nuanced view of risk that is most relevant for risk-averse traders/investors and those focused on minimizing losses.

It should be used in conjunction with other risk and performance measures to gain a more thorough understanding of an investment’s risk profile.

For portfolio construction and risk management, semivariance can allow traders/investors to tailor their portfolios to their specific risk preferences and objectives.