What Happens to Options Values as Interest Rates Rise?

As interest rates rise, the value of call options increases and the value of put options decreases, holding all else equal.

Below we explain why.

Positive Rho for Calls; Negative Rho for Puts

Call options have positive Rho, which means as interest rates increase, call options tend to increase slightly in price, all else held equal.

Put options have negative Rho, which means as interest rates increase, put options tend to decrease slightly in price, all else held equal.

Why do puts and calls have opposite rho sensitivities?

First, higher interest rates can increase the demand for call options because they increase the cost of carrying a long position.

If a trader has to borrow money to put on a long position, they may not want to pay the higher interest, so they will shift into call options (which give them the right to buy the underlying asset at a fixed price), increasing their demand, ceteris paribus.

Conversely, a short position in cash securities provides a cash credit, which can generate interest income.

So this reduces demand for put options in order to capture that interest. Put options give them the right to sell the underlying asset at a fixed price.

Second-Order Effects of Rising Interest Rates

Higher interest rates can affect the volatility of the underlying asset, which can in turn affect the value of options. Volatility is a measure of the amount of uncertainty or risk associated with the price of an asset.

When interest rates rise, the volatility of an asset may increase because cash and bonds start becoming more competitive with the yield on stocks and risk assets, which can cause more market volatility.

This increase in volatility can increase the value of options because it augments the potential for the option to increase in value due to changes in the underlying asset’s price.

What Is The Black-Scholes Formula?

The Black-Scholes formula is a mathematical model used to calculate the theoretical value of an option.

It is a widely used tool in finance and is used to help determine the fair value of an option.

The formula takes into account a variety of factors, including the underlying asset’s price, the option’s exercise price, the time remaining until the option expires, the volatility of the underlying asset, and the risk-free interest rate.

The Black-Scholes formula is named after its creators, Fischer Black and Myron Scholes, who published it in 1973 in their paper “The Pricing of Options and Corporate Liabilities”.

The formula has since become a standard tool used by academics and some finance professionals to evaluate the value of options.

To use the Black-Scholes formula, you need to input the following information:

• The underlying asset’s current price
• The option’s exercise price
• The time remaining until the option expires
• The volatility of the underlying asset
• The risk-free interest rate

Once you have input this information, the formula will calculate the theoretical value of the option.

This value can then be used as a reference point to help determine whether the option is fairly priced or whether it is undervalued or overvalued.

For call options, the rise in r (the risk-free interest rate), causes a rise in the option value, holding all else equal.

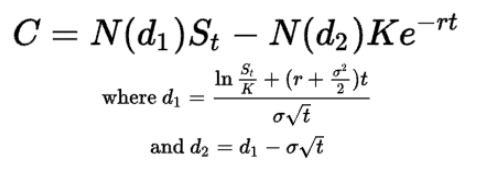
• C = call option price
• N = CDF of the normal distribution
• St = spot price of an asset
• K = strike price
• r = risk-free interest rate
• t = time to maturity